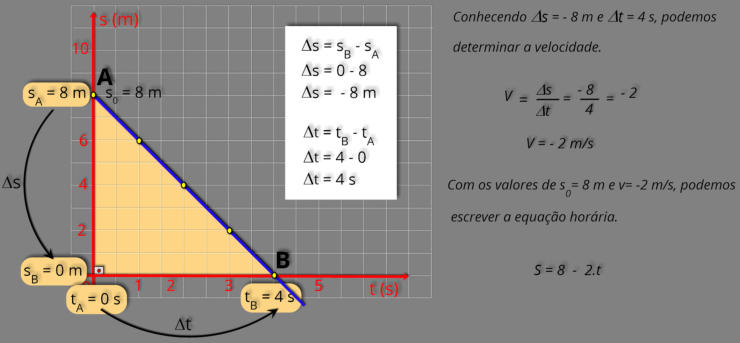
Introdução Vimos anteriormente, que a função que descreve o movimento retilíneo uniforme é dada por: Da   matemática   sabemos   que   a   função   de   posição   do   Movimento   Retilíneo   Uniforme   é   uma   função   do   1º   grau   e   que   quando construímos   um   gráfico,   resulta   em   uma   reta.   Como   exemplo,   vamos   construir   um   gráfico   da   função:    s   =   10   -   4.t   no   sistema internacional (SI). 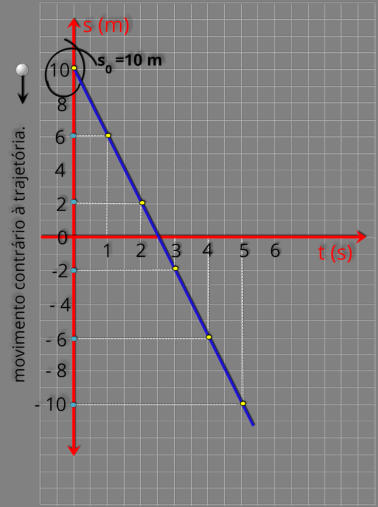Inicialmente    vamos    montar    uma    tabela,    onde    atribuiremos    valores    para    o    tempo    (t),    para    cada    um    destes    valores    de    (t), encontraremos uma posição (s), confira na tabela abaixo o resultado Construindo um gráfico do movimento uniforme Neste exemplo o deslocamento se dá com orientação contrária a trajetória, ou seja, o movimento é retrógrado. O   movimento   retrógrado   é   aquele   em   que   o   corpo   se   desloca   no   sentido   oposto   ao   da   orientação   da   trajetória,   significando   que   a velocidade é negativa. Interpretando um gráfico Agora   que   sabemos   construir   um   gráfico,   faremos   o   caminho   inverso,   ou   seja,   dado   um   gráfico   das   posições   (s)   pelo   tempo   (t), montaremos a sua função horária. 3ª   informação:   Por   último   vamos   determinar   no   gráfico   a   velocidade   do   corpo   que   estamos   estudando,   utilizando   a   expressão   da velocidade média.                                  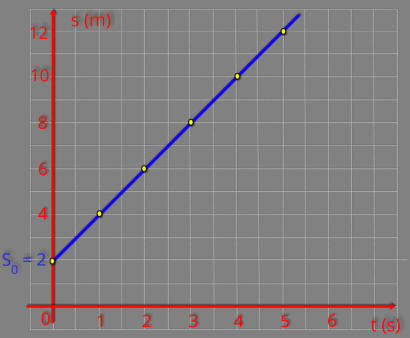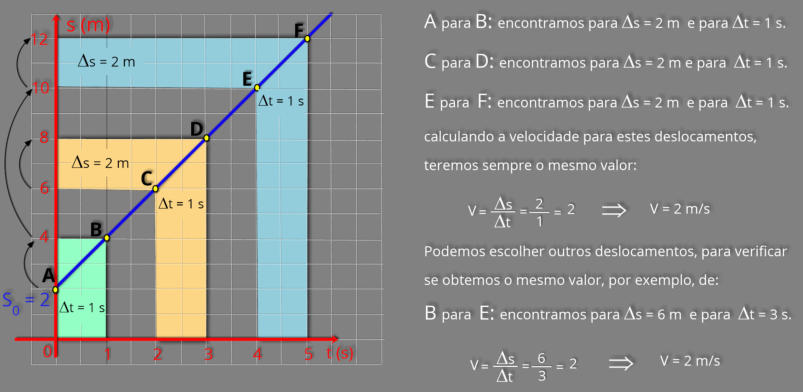Para facilitar a determinação da velocidade, indicamos uma sequência de pontos na reta que denominamos por: A, B, C, D, E e F. Assim, se partirmos de: Em   qualquer   deslocamento   que   realizarmos   no   gráfico,   a   velocidade   terá   o   mesmo   valor,   por   se   tratar   de   um   movimento   retilíneo uniforme. A função horária para este movimento pode ser escrita:                                                                                 s = 2 + 2 t 3ª   informação:   Por   último   vamos   determinar   no   gráfico   a   velocidade   do   corpo   que   estamos   estudando,   utilizando   a   expressão   da velocidade média.                             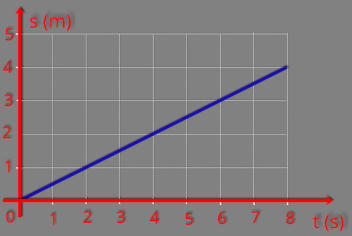Na figura do gráfico vamos indicar alguns pontos que denominamos por: A, B, C e D. Partindo do ponto: Em   qualquer   deslocamento   que   realizarmos   no   gráfico,   a   velocidade   terá   o   mesmo   valor.   A   função   horária   para   este   movimento pode ser escrita:                                                                                             s = 2 + 4 t Inclinação de uma reta no gráfico s x t. Exercícios Resolvidos R1.   Encontre   a   função   horária   que   representa   cada   um   dos   gráficos   abaixo   e   diga   qual   é   o   tipo   de   movimento.   Justifique   suas respostas. 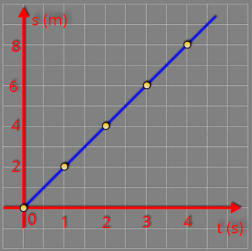a)                                                Vamos   escolher   dois   pontos   (A   e   B)   no   gráfico   para   facilitar   a   determinação   da   velocidade.   Partindo   do   ponto   A   para   o   B,   podemos calcular o valor de   D s e D t , veja a resolução a seguir. Embora   não   tenha   sido   solicitado,   vamos   representar   o   movimento   do   corpo   descrito   pelo   gráfico   em   uma   trajetória,   que   nos   ajudará enxergar melhor o movimento progressivo. 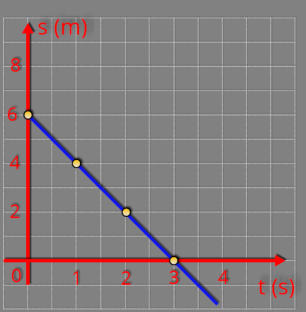b)                                                Escolhemos   dois   ponto   da   reta   (A   e   B)   que   nos   dá   o   valor   de         e   do   correspondente   .   Perceba   que   o   movimento   deste   corpo   é   contrário   a trajetória,   é   um   movimento   retrógrado,   neste   caso      a   velocidade   deverá   ser   negativa.   Veja   como   fica   a   determinação   da   velocidade   deste corpo. Vamos   representar   o   movimento   do   corpo   descrito   pelo   gráfico   em   uma   trajetória,   que   nos   ajudará   enchergar   melhor   o   movimento retrógrado. Exercícios Propostos Gráfico da velocidade pelo tempo Sabemos   que   no   movimento   retilíneo   uniforme   a   velocidade   é   constante,   portanto   o   gráfico   será   uma   reta   paralela   ao   eixo   dos tempos.   No   gráfico   da   velocidade   pelo   tempo,   podemos   encontrar   algumas   informações   importantes   sobre   o   movimento   do corpo. 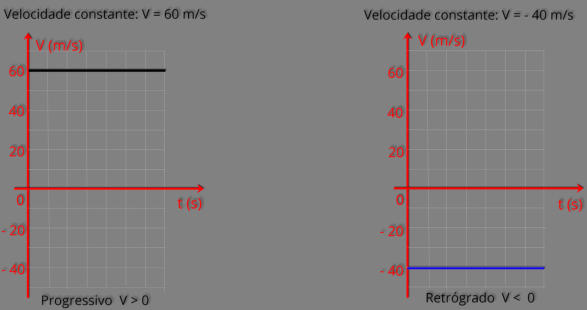Vamos ver dois casos importantes: a) Classificar o movimento em progressivo ou retrógrado. Sabemos que o sinal da velocidade indica se o movimento é progressivo ou retrógrado. b) Determinar a variação de posições do corpo. 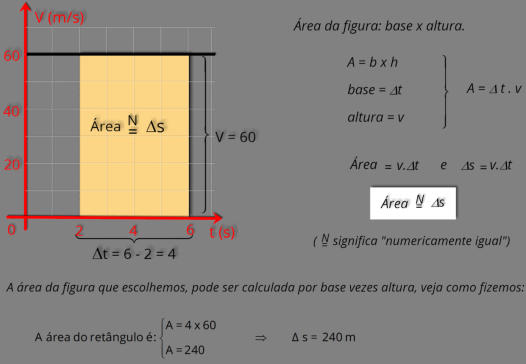O gráfico a seguir representa o movimento de um corpo com velocidade constante de v = 60 m/s. Vejamos como pode ser feito   Exercícios Resolvidos R3. 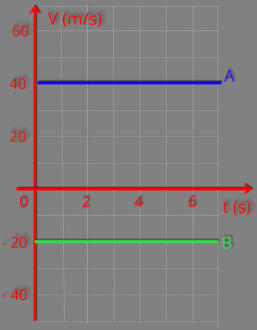Determine para os corpos A e B a variação de posições entre os instantes 0 e 4 s. São dados os gráficos da velocidade escalar em função do tempo. Resolução: Primeiramente vamos separar o gráfico em dois, um com a reta A, e o outro com a reta B. Corpo A                                                                                          Corpo B Resolução:                                                                                    Resolução: Exercícios propostos P4. 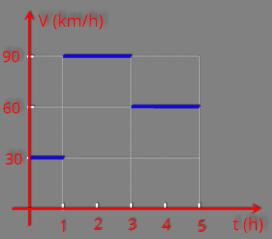(UFCE) Um automóvel move-se numa estrada conforme o gráfico v x t na figura abaixo. Determine sua velocidade média, em km/h, após 5 h. 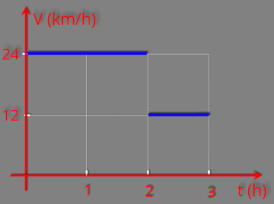P5. O gráfico ao lado representa a velocidade de um ciclista em função do tempo, num  determinado percurso. Determine a velocidade média do ciclista em km/h. 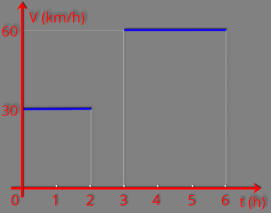P6. Um automóvel faz uma viagem em 6 horas e sua velocidade varia em função do tempo aproximadamente como mostra o gráfico abaixo. Determine a velocidade média do automóvel durante a viagem. P7. O gráfico ao lado representa as posições de um ponto material em movimento como uma função do tempo. Escreva a correspondente função horária do movimento. 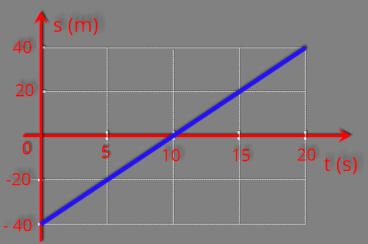P8. Considere um movimento cuja posição s, em função do tempo t, está representada no gráfico. Determine o espaço percorrido pelo móvel entre os instantes t = 0 s e t = 20 s, em metros.

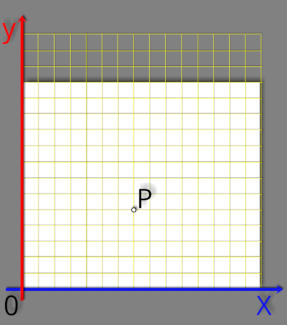
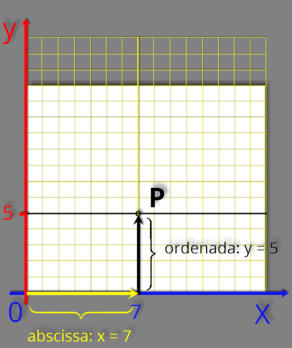
O Plano cartesiano O    primeiro    passo    para    aprendermos    como    se constrói   um   gráfico,   é   saber   localizar   um   ponto   em uma região. Na figura, indicamos o ponto P. Você   terá   certa   dificuldade   em   dizer   qual   é   a   sua posição   em   uma   região,   que   no   nosso   caso   possui   o formato   de   um   quadrado.   Esta   situação   nos   leva   à necessidade    de    criarmos    regras    para    dar    a    sua localização. Uma   maneira   que   facilitaria   bem   o   nosso   trabalho na    localização    do    ponto    P    seria    quadricular    o plano. Observe como ficou a figura. O      procedimento      que      estamos      adotando      foi idealizado      pelo      físico      e      matemático      francês Descartes. Adotando   a   ideia   de   Descartes,   vamos   determinar   a distância   do   ponto   P   em   relação   a   dois   eixos   que   se cruzam   perpendicularmente,   como   pode   ser   visto na figura. Estes   dois   eixos   perpendiculares,   onde   o   horizontal chamamos   de   eixo   das   abscissas   (eixo   x),   e   o   da vertical eixo das ordenadas (eixo y). 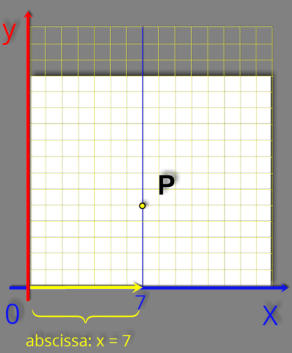Ao     nos     deslocarmos     pelo     eixo     das     abscissas, partindo     da     origem,     verificamos     que     o     nosso deslocamento é de x = 7 unidades. Na   vertical,   nos   deslocamos   em   direção   ao   ponto   P, caminhando    5    unidades    ou    5    quadrados,    que significa dizer que  y = 5. 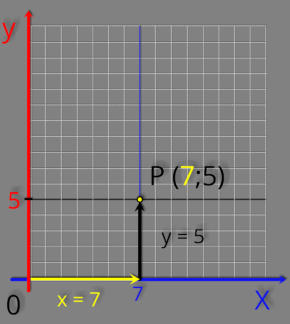Assim    mostramos    como    pode    ser    localizado    um ponto   no   Plano,   ou   seja,   ele   fica   determinado   pela sua     abscissa     e     pela     sua     ordenada,     o     qual chamamos de coordenadas do ponto P. Quando    queremos    marcar    um    ponto    no    plano cartesiano,   para   evitar   confusão   seguiremos   uma regra:   primeiro   o   avanço   horizontal   (x)   e   depois   o vertical (y). 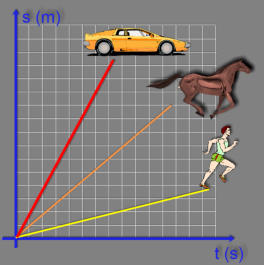P (abscissa ; ordenada ) =  P ( x ; y ) =  P ( 7; 5 ) Quem é mais veloz? A    inclinação    de    um    gráfico    de    posição    (s)    pelo tempo   (t)   nos   fornece   a   velocidade.   A   reta   para   um corpo    com    maior    velocidade    (carro),    possui    uma inclinação    maior.    Para    uma    velocidade    pequena (homem correndo) a reta é menos inclinada. Quanto    menor    for    a    velocidade    mais    a    reta    se aproxima do eixo (t) na horizontal. 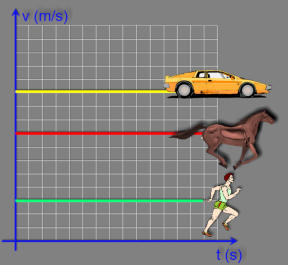(Gráfico fora de escala) O    movimento    é    chamado    uniforme    quando    a velocidade      for      constante.      Quanto      maior      a velocidade,   mais   alto   se   localiza   a   reta   (carro).   Se   a reta    se    aproxima    do    eixo    x,    sua    velocidade    se aproxima do zero. (Gráfico fora de escala) Lembrando algumas área importantes.

A   partir   da   origem   dos   eixos   x   e   y,   marcamos   os   valores   do tempo   no   eixo   x   (das   abcissas)   -   variável   independente. Em    seguida    marcaremos    no    eixo    y    (das    ordenadas)    - variável   dependente   -,   o   eixo   das   posições   (s).   Seguindo esta regra, teremos como resultado o gráfico a seguir. Analisando    o    gráfico,    observamos    que    em    t    =    0    s,    a posição   do   corpo   é   s   =   10   m   portanto   a   posição   inicial   é   s 0 =   10   m.   Quanto   ao   deslocamento   do   corpo,   ele   é   contrário ao da trajetória, passando pelo marco zero. 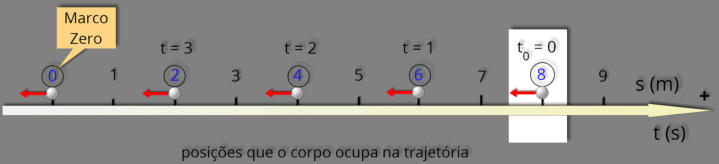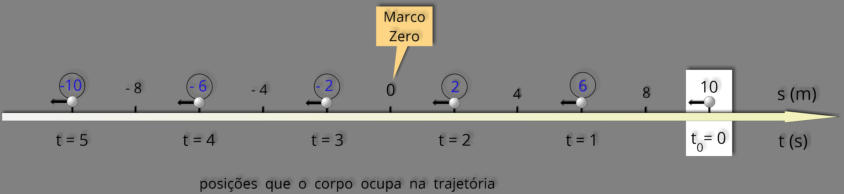Uma      outra      forma      para      representar      este      mesmo movimento,     pode     ser     feito     através     do     desenho     da trajetória,    indicando    sua    posição    inicial    e    as    sucessivas posições e o instante em que isto ocorre.

1º exemplo Vamos       determinar       no       gráfico       a       seguir,       a       sua correspondente função horária de posição. Podemos   tornar   a   resolução   deste   exercício   mais   simples   se formos     organizados,     vamos     então     seguir     3     etapas     que simplificarão a resolução: 1ª     informação:     O     gráfico     é     uma     reta,     sabemos     da matemática   que   a   função   expressa   por   uma   reta   é   de   1º grau,   característica   do   movimento   uniforme.   Na   cinemática a função é:                                                 s = s 0 + v.t. 2ª   informação:   Em   t   =   0   s,   s   =   2   m,   portanto   é   o   início   da trajetória, ou seja, s 0 = 2 m. A função ficará assim:                                             s = 2 + v.t.

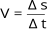
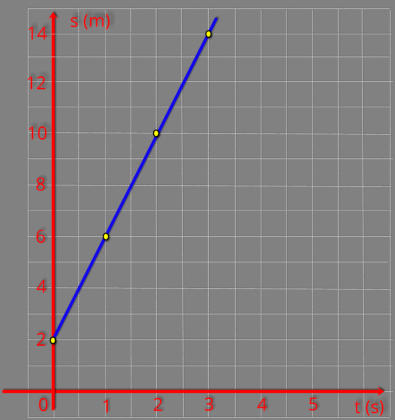
2º exemplo Vamos       determinar       no       gráfico       a       seguir,       a       sua correspondente função horária de posição. Podemos   tornar   a   resolução   deste   exercício   mais   simples   se formos     organizados,     vamos     então     seguir     3     etapas     que simplificarão a resolução: 1ª   informação:   O   gráfico   é   uma   reta,   característica   de   uma função   do   1º   grau,   característica   do   movimento   uniforme. Na cinemática a função é:                                                                        s = s 0  + v.t. 2ª   informação:    Em   t   =   0   s   a   posição   é      s   =   2   m,   portanto   é   o início da trajetória, ou seja, s 0 = 2 m, a função ficará assim:                                                                                                                                      s = 2 + v.t.

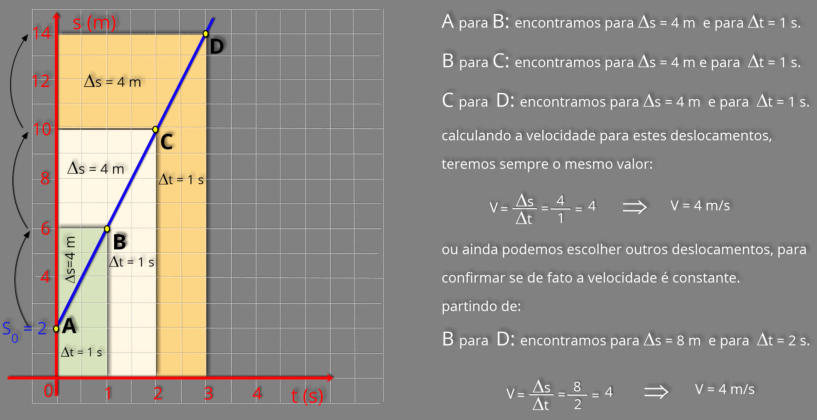
Partindo   dos   dois   exemplos   que   acabamos   de   fazer,   podemos   ainda tirar   mais   informações   do   gráfico:   o   significado   da   inclinação   destas retas. Construindo   as   duas   retas   no   mesmo   plano   cartesiano,   verificamos que   a   origem   delas   é   a   mesma,   indicando   que   os   dois   movimentos possuem   a   mesma   posição   inicial,   isto   é,   s 0    =   2   m.   No   entanto   as inclinações   são   diferentes.   Indicamos   a   inclinação   pelo   ângulo   que   a reta faz com o eixo dos tempos ( t ). Analise a figura a seguir. 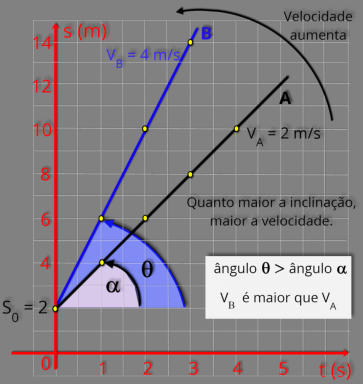A   reta   mais   inclinada,   ou   seja,   aquela   que   possui   o   maior   ângulo   de inclinação   (   q   )   possui   também   o   maior   valor   para   a   velocidade.   Por sua   vez   a   reta   que   possui   uma   menor   inclinação,   (   a   )   terá   também uma menor velocidade. A   conclusão   que   chegamos   é   que,   quanto   maior   a   inclinação,   maior será a velocidade.

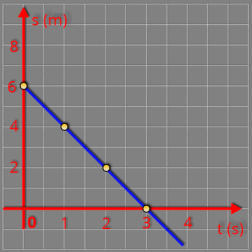
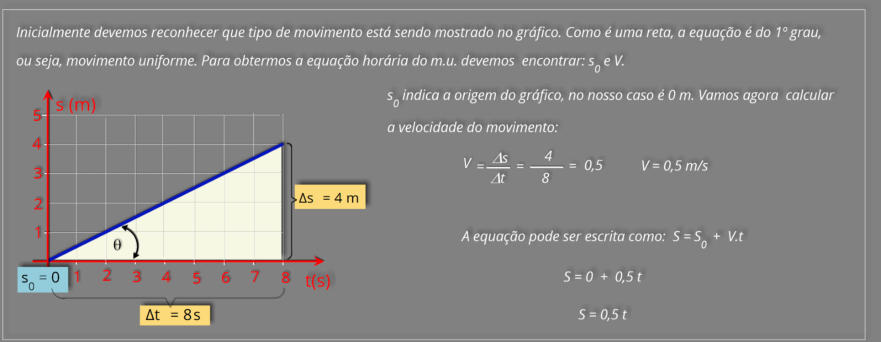
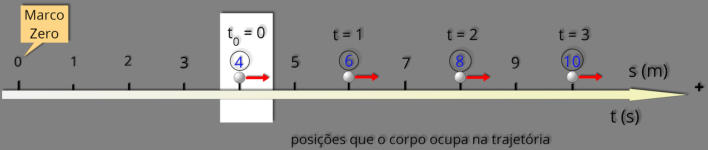
Resolução Para   encontrarmos   a   função   horária   do   movimento,   vamos   seguir   3 etapas: 1ª   informação:   O   gráfico   é   uma   reta,   indicando   que   é   uma   função nestes casos é do 1º grau, característica do movimento uniforme. 2ª   informação:    Em   t   =   0   s   a   posição   é   s   =   4   m,   portanto   é   o   início   da trajetória, ou seja, s0 = 4 m, a função ficará assim                                           s = 4 + v.t.                                                                                                     3ª   informação:   Por   último   vamos   determinar   no   gráfico   a   velocidade   do corpo   que   estamos   estudando,   utilizando   a   expressão   da   velocidade média.

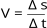
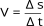
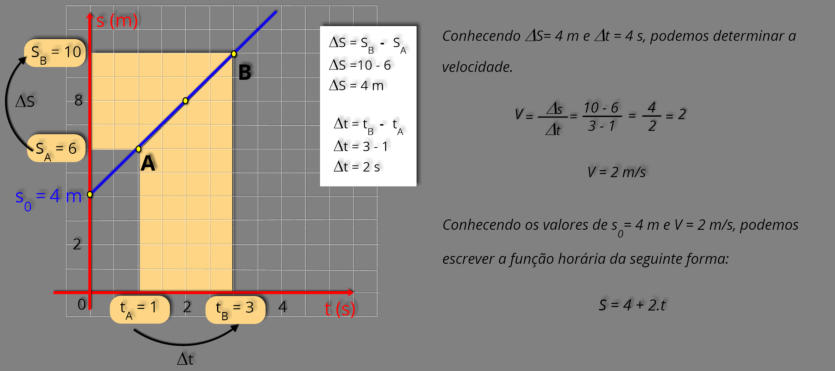
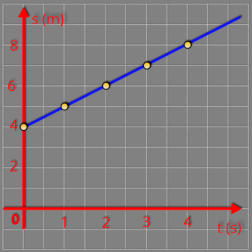
Resolução Para encontrarmos a função horária do movimento, vamos seguir 3 etapas: 1ª   informação:   O   gráfico   é   uma   reta,   característica   de   uma   função   do   1º   grau, característica do movimento uniforme. 2ª   informação:    Em   t   =   0   s   a   posição   é   s   =   8   m,   portanto   é   o   início   da   trajetória, ou seja, s 0 = 8 m, a função ficará assim                                                         s = 8 + v.t                                                                                                                                                                                                                              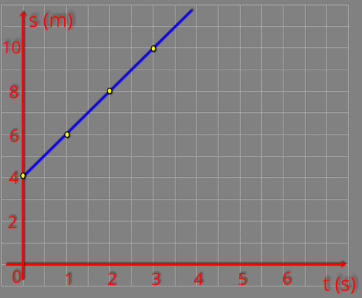3ª   informação:   Através   da   reta   podemos   determinar   a   velocidade   do   corpo   que estamos estudando, utilizando a expressão da velocidade média.

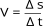
P1.    Um    corpo    movimenta-se    sobre    uma    trajetória    retilínea    com    velocidade constante,   representado   pelo   gráfico   posição   em   função   do   tempo,   onde   a   posição e    o    tempo    estão    de    acordo    com    o    Sistema    Internacional.    Determine    a    função horária deste movimento. P2.   Passeando   com   sua   bicicleta,   ao   longo   de   um   trecho   retilíneo   de   uma   ciclovia,   o ciclista   consegue   manter   a   velocidade   constante.   O   diagrama   da   posição   em   função do   tempo   é   mostrado   na   figura   abaixo.   Considerando   que   as   unidades   adotadas são do Sistema Internacional, Determine a função horária deste movimento. P3.   O   gráfico   a   seguir   representa   a   posição   em   função   do   tempo   de   uma   partícula em   movimento   retilíneo   uniforme   sobre   o   eixo   x.   Considerando   que   as   unidades adotadas     são     do     Sistema     Internacional,     Determine     a     função     horária     deste movimento.

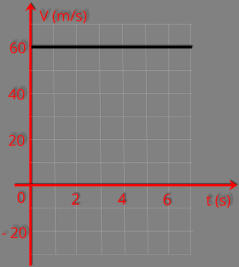
É   possível   determinar   em   um   gráfico   v   x   t,   o   deslocamento   realizado   pelo   corpo. Como   exemplo   vamos   calcular   o   deslocamento   do   corpo   representado   pelo   gráfico acima, entre os instantes t 1 = 2 s e t 2 = 6 s.  A   determinação   do   deslocamento   está   associada   a   área   da   figura   que   encontramos entre os dois instantes escolhidos.

Podemos     então     afirmar     que     o     valor numérico    da    área,    corresponde    ao    valor do deslocamento  D s . No    nosso    exemplo    podemos    determinar qual   foi   o   deslocamento   sofrido   entre   os instantes t 1 = 2 s e t 2 = 6 s.