A maior parte das imagens utilizadas neste site pertencem a terceiros, que gentilmente permitiram
sua utilização, assim sendo, não podemos autorizar a utilização das imagens deste site.
© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Física para o
Ensino Médio
1.8 Notação científica
Índice das aulas de física
1.8.a Para que serve a notação científica?
A
primeira
tentativa
conhecida
em
representar
números
muito
grandes
foi
realizada
pelo
matemático
grego
Arquimedes,
encontramos
este
estudo
na
sua
obra
O
Contador
de
Areia,
no
século
III
a.C.
Neste
trabalho,
dirigindo
se
ao
rei
Gelão,
o
siracusano
inicia
o
tratado
discorrendo
sobre
a
questão
do
infinito
e
dos
números
extremamente
grandes,
usando
o
número
de
grãos
de
areia
como
exemplo.
Arquimedes
demonstra
que
consegue
escrever
o
número
de
grãos
de
areia
necessários
para
encher
a
esfera
que
tem
por
centro
o
sol
e
cujo
raio
é
a
distância
entre
o
centro
do
sol
e
o
centro
da
terra,
ou
seja,
o
número
de
grãos
de
areia
que
o
'universo',
pode
conter.
Para
poder
demonstrar
a
sua
tese,
Arquimedes
teve
de
se
basear
em
estimativas
de
distâncias
entre
a
Terra
e
a
Lua,
e
entre
a
Terra
e
o
Sol.
Ele
desenvolveu
um
método
de
representação
numérica
para
estimar
quantos
grãos
de
areia
seriam
necessários
para preencher o universo. O número estimado por ele, escrito em notação científica hoje, seria de 1 × 10
63
grãos.
Notação
científica
é
uma
forma
muito
conveniente
para
escrever
pequenos
ou
grandes
números
e
realizar
cálculos
com
eles.
Em
algumas
áreas
da
ciência,
trabalhar
com
números
muito
grandes,
como
é
o
caso
da
astronomia,
ou
muito
pequenas
no
estudo
dos
átomos.
3
3
2
2
2
1
0
0
,
0
0
2
1
0
1
0
1
0
1
0
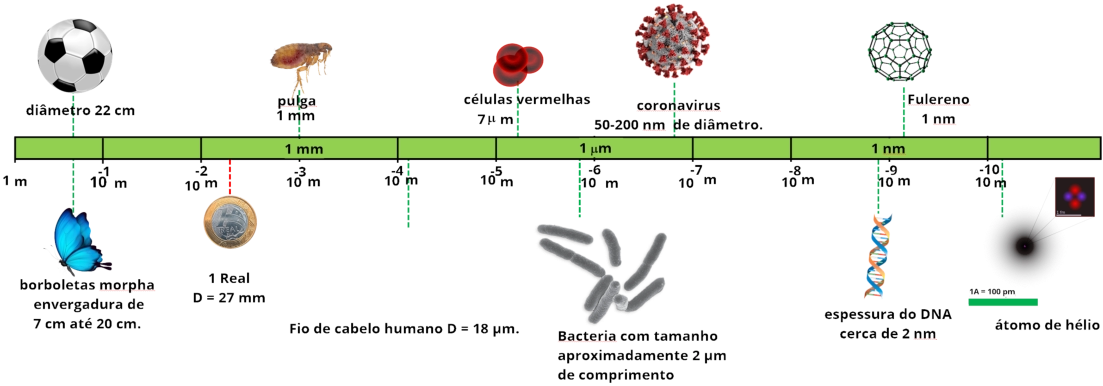
Para
fazer
comparações
de
tamanho,
a
sequência
tem
início
com
uma
bola
de
futebol
de
campo,
gradativamente
vai
diminuindo
até
chegar
nas
dimensões
do átomo. Neste exemplo estamos comparando distâncias, e utilizando a notação científica.
O
sistema
decimal,
que
se
baseia
no
número
10,
é
o
sistema
numérico
mais
utilizado
no
mundo.
Ao
usar
o
sistema
decimal
na
base 10, o expoente informa quantas vezes devemos multiplicar 10 por ele mesmo: por exemplo, 10 elevado à terceira potência (10
3
) é
10
3
= 10 x 10 x 10 = 1 000 ou 10
4
= 10 x 10 x 10 x 10 = 10 000
quando o expoente for negativo, quantas vezes devemos dividir por 10, como:
A potência de dez é utilizada para abreviar múltiplos de dez, ou submúltiplos de dez. Assim:
Voltando ao problema de Arquimedes, o número de grãos de areia seria escrito hoje como: 1 × 10
63
.
Perceba que o valor do
expoente é 63, escrever este número de forma completa, significa escrever o valor numérico, 1 e em seguida mover a vírgula para a
direita em 63 casas decimais, preenchendo os novos espaços com zeros. O resultado seria o seguinte;
G = 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
perceba que não faz sentido realizar cálculos com um número com tantos zeros. Vejamos outro exemplo, a massa do elétron é:
m = 0,000 000 000 000 000 000 000 000 000 000 910 kg.
Esse número é realmente muito pequeno! Se você tivesse que escrevê-los várias vezes, ou pior ainda, usá-lo para realizar
cálculos, teria problemas com todos esses zeros. Estes dois exemplos nos mostram, que é muito mais simples expressá-los usando
notação científica, ou seja a melhor maneira de lidar com números grandes ou pequenos, é abreviá-los usando potências de dez.
Como isso pode ser feito?
A notação científica consiste em escrever certa grandeza como o produto de um número N, igual ou maior que
1, e menor que 10
( 1≤ N < 10 ), multiplicado por 10 elevado a alguma potência
Assim o valor m = 0,000 000 000 000 000 000 000 000 000 000 910 kg, pode ser escrito como 9,1 x 10
31
kg. Como isso é feito? É
o que veremos a seguir.
1.8.b Escrevendo em notação científica
Exemplo 1.
Vejamos como transformar a grandeza: G = 253756,42 kg, em notação científica, seguindo o modelo:
G = N x 10
n
A
notação
científica
padronizada
exige
que
N
seja
um
valor
maior
igual
a
1
e
menor
que
dez
(1
≤
N
<10).
Seguindo
este
critério
devemos escrever:
N = 253756
,
42 deverá ser escrito como: 2
,
5375642 de acordo com a regra, teremos 1 ≤ 2,5375642 < 10
Observe
que
a
mudança
da
virgula
reduziu
o
valor
numérico
de
N.
Algo
deve
ser
feito
para
não
alterar
o
valor
numérico
de
N.
Assim
teremos que:
"Cada casa decimal que diminui o valor de N, aumenta o expoente em uma unidade".
Observe que ao deslocar a vírgula 5 casas reduzindo o valor numérico de N, o expoente de dez 10, deverá aumentar onde n = +5.
Exemplo 2.
Vamos
escrever
a
grandeza
fisica
do
comprimento:
G
=
0,000
000
0475
m,
de
acordo
com
a
notação
científica,
seguindo
o
modelo
adotado :
G = N x 10
n
A
escrita
em
notação
científica
exige
que
N
seja
igual
ou
maior
que
1,
e
menor
que
dez,
ou
seja:
1
≤
N
<10
,
desta
forma
devemos
fazer
esta transformação:
N = 0,000 000 0475 m deverá ser escrito como: 4,75 m de acordo com a regra, onde 1 ≤ 4,75 < 10
Observe
que
a
mudança
da
virgula
alterou
o
valor
numérico
de
N.
Algo
deve
ser
feito
para
não
alterar
o
valor
numérico
de
N.
Recordando
a
regra
teremos
que:
"Cada
casa
decimal
que
aumenta
o
valor
de
N,
deveremos
diminuir
o
expoente
n
em
uma
unidade".
Observe
que
ao
deslocar
a
vírgula
8
casas,
você
alterou
o
valor
numérico
original
tornando-o
maior,
então,
para
compensar
esta
alteração, você deve alterar o expoente n negativo. Nesse caso, o expoente é n = - 8.
Exemplo 3.
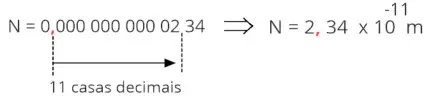
Vamos escrever o valor da massa G = 0,000 000 000 0234 kg em notação científica. Seguindo o
modelo:
G = N x 10
n
Novamente N deve obedecer um valor entre 1 ≤ N <10, ou seja, um número igual ou maior que 1 e menor que 10. Teremos:
N =
0,000 000 000 0234
deverá ser escrito como: 2,34 de acordo com a regra, onde 1 ≤ 2,34 < 10
Observe
que
a
mudança
da
virgula
alterou
o
valor
numérico
de
N.
Recordando
a
regra:
"Cada
casa
decimal
que
aumenta
o
valor
de
N, deveremos diminuir o expoente n em uma unidade".
Neste
caso
a
vírgula
será
deslocada,
11
casas
para
a
direita,
aumentando
o
valor
numérico,
assim
devemos
compensar
diminuindo
o
valor do espoente. Neste caso n =
-
11.
Exemplo 4.
A
massa
do
próton
é
aproximadamente
M
=
G
=
0,000
000
000
000
000
000
000
000
00167
kg,
vamos
escrever
este
valor
de
acordo
com a notação científica, sguindo o
modelo:
G = N x 10
n
Vamos
fazer
com
que
N
seja
um
valor
entre
1
≤
N
<10,
ou
seja,
um
número
igual
ou
maior
que
1,
e
menor
que
10.
Obedecendo
este
critério teremos:
Neste
caso
a
vírgula
será
deslocada,
27
casas
para
a
direita,
aumentando
o
valor
numérico,
assim
devemos
compensar
diminuindo
o
valor
do
espoente.
"Cada
casa
decimal
que
aumenta
o
valor
de
N,
deveremos
diminuir
o
expoente
n
em
uma
unidade".
Neste
caso n =
-
27.
Exemplo 5.
A massa da Terra é de aproximada de Massa = 5 973 600 000 000 000 000 000 000 kg. Vamos escrever na forma:
G = N x 10
n
Vamos
fazer
com
que
N
seja
um
valor
entre
1
≤
N
<10,
ou
seja,
um
número
igual
ou
maior
que
1,
e
menor
que
10.
Obedecendo
este
critério teremos:
Observe
que
ao
deslocar
a
vírgula
24
casas,
o
valor
numérico
será
reduzindo,
para
conpensar
esta
alteração
o
expoente
de
dez
10,
deverá aumentar onde n = +24.
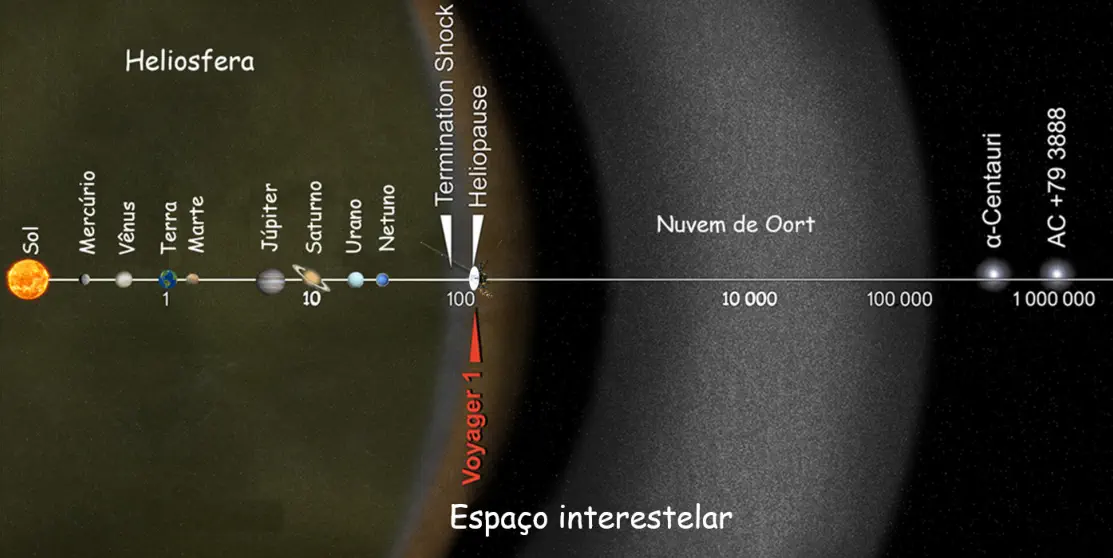
1.8.c Unidades de medida na astronomia
Os
astrônomos
usam
a
distância
entre
a
Terra
e
o
Sol,
que
é
de
150
milhões
de
quilômetros,
como
uma
unidade
de
medida
chamada
Unidade Astronômica 1,0 UA.
1 unidade astronômica = 149 597 870 700 metros (por definição)
O
ano-luz
é
uma
unidade
de
comprimento
usada
para
expressar
distâncias
astronômicas
e
é
equivalente
a
cerca
de
9,46
trilhões
de
quilômetros
(9,46
×
10
12
km).
Conforme
definido
pela
União
Astronômica
Internacional
(IAU),
um
ano-luz
é
a
distância
que
a
luz
viaja
no vácuo em um ano juliano (365,25 dias).
1 ano luz = 9 460 730 472 580 800 metros (exatamente)
Podemos realizar o cálculo para termos idéia de como este valor é obtido.
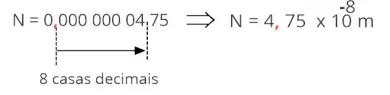


7
7
1
a
n
o
3
6
5
di
a
s
1
a
n
o
3
1
5
3
6
0
0
0
s
3
,
1
5
3
6
0
0
1
0
s
3
,
1
6
1
0
s
1
di
a
8
6
4
0
0
s
8
8
8
7
15
7
7
15
c
3
,
0
x
1
0
m
/
s
s
s
s
?
v
3
,
0
x
1
0
s
3
,
0
x
1
0
3
,
1
6
1
0
9
,
5
1
0
m
t
3
,
1
6
1
0
t
3
,
1
6
1
0
s
1
a
n
o
l
u
z
s
9
,
5
1
0
m
va
l
o
r
a
p
r
o
x
i
m
a
d
o
1 UA

10 UA

Planetas
Distância em milhões
de quilômetros do Sol
Distância do sol em
UA
Tempo que a luz leva
Mercúrio
57
0,39
3,2 minutos
Vênus
108
0,72
6,1 minutos
Terra
149
1,00
8,7 minutos
Marte
228
1,52
12,9 minutos
Júpiter
780
5,20
44,2 minutos
Saturno
1437
9,53
1,4 horas
Urano
2871
19,10
2,7 horas
Netuno
4530
30,00
4,3 horas
Veja na tabela como ficam as distâncias dentro do sistema solar.
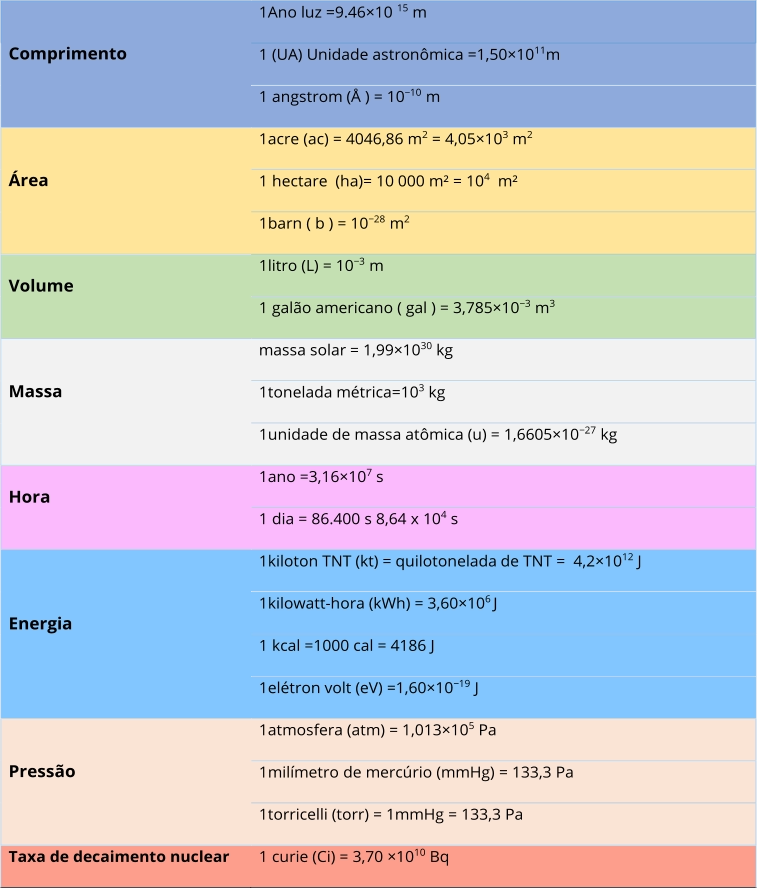
Valores utilizados em física em notação científica
Vamos praticar
a importância em medir




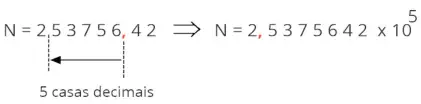
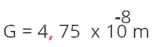
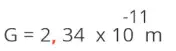
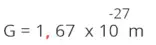
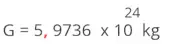
Bases
da
Física