






© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física
2.5 Equações horárias no movimento retilíneo uniformemente variado

Cinemática

Montanha russa
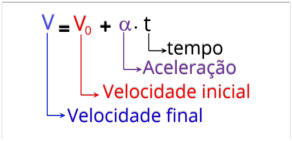
2.5.a Equações horárias do MRUV - Velocidade
Vamos inicialmente, estabelecer uma relação entre a velocidade de um corpo, e o tempo. Esta expressão denominamos de
função horária da velocidade.
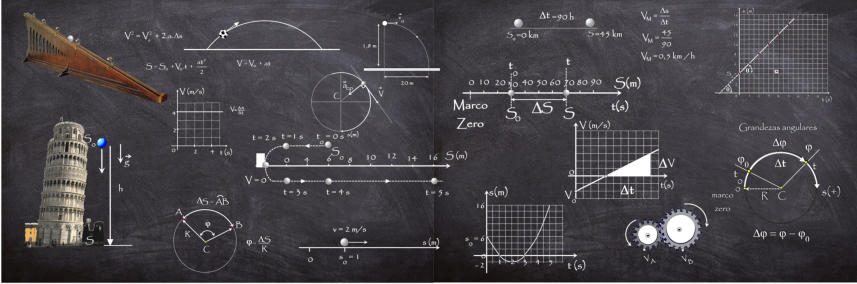
A função horária da velocidade vem da expressão da aceleração, que pode ser obtida da seguinte forma:
Vamos considerar que o início do movimento ocorra no instante
t
0
= 0 s
. A equação horária da velocidade fica:
Melhorando a equação, teremos a equação horária da velocidade.
2.5.b Exercícios resolvidos
R1.
A velocidade de um corpo que executa MRUV, é dada pela expressão v = 6 - 2t em unidades do (SI). Determine:
a) a velocidade inicial do corpo;
Resolução:
Comparando a equação da velocidade com a equação fornecida pelo exercício, teremos
b) a aceleração do corpo:
Resolução:
Para encontrar a aceleração, faremos novamente a comparação das equações.
c) a velocidade do corpo no instante t = 8 s
Resolução:
Devemos
neste
item
determinar
qual
deve
ser
a
velocidade
do
corpo
no
instante
t
=
8
s.
Substituindo
o
valor
do
tempo
na
equação,
teremos:
R2.
Numa
rodovia,
um
motorista
dirige
com
velocidade
v
=
20
m/s
quando
avista
um
animal
atravessando
a
pista.
Assustado,
o
motorista freia bruscamente e consegue parar em 5,0 segundos, a tempo de evitar o choque. Determine:
a) a aceleração média de frenagem em m/s
2
;
Resolução:
Para determinar a aceleração do movimento, devemos ver quais são as grandezas físicas fornecidas pelo exercício:
b) a equação horária da velocidade para este veículo.
Resolução:
Sabemos que a equação horária da velocidade é: v = v
0
+ t, substituindo os valores teremos:
2.5.c Exercícios Propostos
P1.
Uma
automóvel
parte
do
repouso
com
aceleração
constante
de
3
m/s
2
.
Determine
em
que
instante
ele
atingiu
a
velocidade
de
30
m/s.
P2.
Uma partícula em movimento retilíneo movimenta-se de acordo com a equação V = 7 + 2t, no (SI). Determine para essa partícula:
a) A velocidade inicial
b) A aceleração
c) A velocidade quando t = 4 s.
P3.
Um
automóvel
que
trafega
com
velocidade
constante
de
10
m/s,
em
uma
pista
reta
e
horizontal,
passa
a
acelerar
uniformemente
à
razão
de
60
m/s
a
cada
minuto,
mantendo
essa
aceleração
durante
30
segundos.
Determine
a
velocidade
instantânea do automóvel ao final desse intervalo de tempo.
P4.
No instante t
0
= 0 s, um automóvel a 72 km/h passa a frear com aceleração escalar constante igual a 4 m/s
2
. Determine:
a) a função horária de sua velocidade escalar;
b) o instante em que sua velocidade escalar se anula.
P5.
(UFRJ)
Um
avião
vai
decolar
em
uma
pista
retilínea.
Ele
inicia
seu
movimento
na
cabeceira
da
pista
com
velocidade
nula
e
corre
por
ela
com
aceleração
média
de
2,0
m/s
2
até
o
instante
em
que
levanta
voo,
com
uma
velocidade
de
80
m/s,
antes
de
terminar
a
pista. Calcule quanto tempo o avião permanece na pista desde o início do movimento até o instante em que levanta voo.
P6.
(UNESP)
Um
veículo
está
rodando
à
velocidade
de
36
km/h
numa
estrada
reta
e
horizontal,
quando
o
motorista
aciona
o
freio.
Supondo
que
a
velocidade
do
veículo
se
reduz
uniformemente
à
razão
de
4
m/s
em
cada
segundo
a
partir
do
momento
em
que
o
freio foi acionado, determine o tempo decorrido entre o instante do acionamento do freio e o instante em que o veículo para.
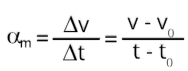
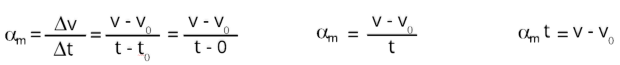
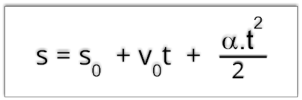




2
0
0
0
v
0
m
/
s
(
r
e
p
o
u
s
o
)
v
v
0
2
0
2
0
v
v
2
0
m
/
s
4
m
/
s
t
t
t
5
5
t
5
s
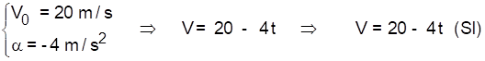
2.5.d Equação horária de posição
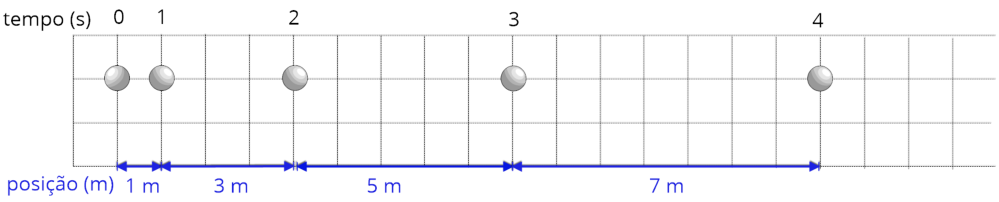
A
figura
abaixo
representa
o
movimento
de
um
corpo
e
nos
indica
as
sucessivas
posições
que
ele
ocupa
e
o
instante
em
que
elas
ocorrem.
Entre
uma
posição
e
outra,
o
intervalo
de
tempo
se
mantém
constante
de
t
=
1
s,
por
sua
vez
as
distâncias
percorridas
são
cada
vez
maiores.
Se
o
corpo
percorre
distâncias
cada
vez
maiores
no
mesmo
intervalo
de
tempo,
sugere-se
que
a
velocidade
não
é
constante
e
tem
seu
valor
aumentado.
Neste
caso
a
velocidade
varia
uniformemente
caracterizando
um
movimento
retilíneo uniformemente variado.
Na
cinemática,
observar
um
movimento
é
fundamental,
porém
o
que
se
pretende
é
poder
expressar
através
de
uma
função
matemática
tudo
aquilo
que
dissemos
baseando-se
na
figura.
Esta
função
horária
de
posição,
nos
dará
a
cada
instante
(t),
a
posição
(s) do corpo. Por se tratar do movimento uniformemente variado, esta função é de segundo grau, dada por:

2.5.e Exercícios resolvidos
R3.
(EEM)
Um
móvel
passa
pelo
marco
zero
de
uma
trajetória,
em
movimento
retrógrado
uniformemente
retardado,
no
instante
t
=
0
s. Nesse instante, sua velocidade escalar é 20 m/s e a aceleração escalar é 4 m/s
2
, em módulo. Determine sua posição e velocidade:
a) para t = 5,0 s.
Resolução:
Para
resolvermos
o
problema,
devemos
obter
a
equação
de
posição
e
da
velocidade.
Vamos
inicialmente
escolher
os
valores
necessários para montar as equações.
b) para t = 10 s.
Resolução:
R4.
(FAU-USP)
Partindo
do
repouso
no
instante
t
=
0,
um
ponto
material
possui
aceleração
escalar
constante
e
igual
a
2,0
m/s
2
.
Qual
a distância percorrida entre os instantes t
1
= 1,0 s e t
2
= 2,0 s ?
Resolução:
Vamos inicialmente identificar os valores numéricos fornecidos no problema:

2.5.f Exercícios propostos
P7.
(UFSC)
Um
móvel
descreve
um
movimento
retilíneo
uniformemente
acelerado
numa
trajetória
em
linha
reta
e
suas
posições
variam
no
tempo
de
acordo
com
a
equação
s
=
20
+
2
t
+
2t
2
,
onde
s
é
medido
em
metros
e
t
em
segundos.
Determine
a
velocidade
do
móvel quando o tempo t for igual a 10 s.
P8.
(UFPE)
Uma
partícula
se
move
ao
longo
do
eixo
x
de
modo
que
sua
posição
é
descrita
por
x
(t)
=
-
10,0
+
2,0
t
+
3,0
t
2
,
onde
o
tempo
está
em
segundos
e
a
posição,
em
metros.
Calcule
o
módulo
da
velocidade
média,
em
metros
por
segundo,
no
intervalo
entre
t =1,0s e t = 2,0 s.
P9.
A
função
horária
da
posição
s
de
um
móvel
é
dada
por
s
=
20
+
4t
-
3t
2
,
com
unidades
do
Sistema
Internacional.
Nesse
mesmo
sistema, escreva a função horária da velocidade deste móvel.
P10.
(EEM)
Um
móvel
passa
pelo
marco
zero
de
uma
trajetória,
em
movimento
retrógrado
uniformemente
retardado,
no
instante
t
=
0
s.
Nesse instante, sua velocidade escalar é 20 m/s e a aceleração escalar é 4 m/s
2
, em módulo. Determine sua posição e velocidade:
a) para t = 5,0 s.
b) para t = 10 s
P11.
A velocidade de um corpo que executa MRUV, é dada pela expressão v = 4 + 3t em unidades do (SI). Determine:
a) a velocidade inicial do corpo;
b) a aceleração do corpo;
c) a velocidade do corpo no instante t = 8 s
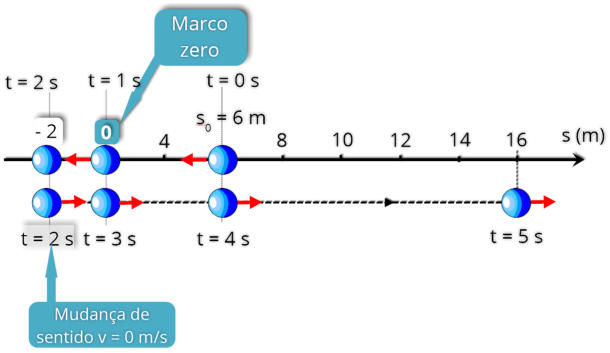
2.5.g Mudança de sentido
Em
algumas
situações
um
corpo
ao
executar
um
MRUV,
pode
mudar
seu
sentido
durante
o
movimento.
O
exemplo
da
figura
abaixo,
mostra
que
a
posição
inicial
é
s
0
=
6
m,
e
seu
deslocamento
é
contrário
a
trajetória.
Quando
o
corpo
atinge
a
posição
s
=
-
2
m
no
instante
t
=
2
s,
ocorre
a
mudança
de
sentido,
e
seu
movimento
passa
a
ser
favorável
a
trajetória.
Esta
posição
de
inversão
do
movimento ocorre quando sua velocidade for nula
Matematicamente
para
determinar
o
instante
em
que
ocorre
a
mudança
de
sentido,
atribuímos
a
velocidade
o
valor
nulo v = 0 m/s.
Veja como fica:
V= -8 + 4 t
quando muda de sentido:
V = 0
2.5.h Exercícios resolvidos
R5.
A
velocidade
de
um
corpo
que
executa
MRUV,
é
dada
pela
expressão
v
=
-
4
+
2t
em
unidades
do
(SI).
Determine o instante em que o corpo muda seu sentido.
Resolução:
Sabemos que a condição para que o corpo mude seu sentido, a velocidade deve ser nula (v = 0 m/s)
v = - 4 + 2t substituindo: V = 0 m/s portanto 0 = - 4 + 2t 4 = 2t o instante será:
t = 2 s

R6.
A
função
horária
da
posição
s
de
um
móvel
é
dada
por
s
=
20
+
4t
-
3t
2
,
com
unidades
do
Sistema
Internacional.
Nesse
mesmo
sistema;
a) escreva a função horária da velocidade deste móvel.
Resolução:
b) encontre o instante em que o corpo muda de sentido
Resolução:
Sabemos que a condição para que o corpo mude seu sentido, a velocidade deve ser nula (v = 0 m/s) v = 4 - 6 t, substituindo
0 = 4 - 6 t - 4 = - 6 t o instante será: t = 4/6 s
2.5.j Exercícios propostos
P12.
Partindo
da
posição
s
0
=
2
m
no
instante
t
=
0
s,
com
uma
velocidade
v
0
=
2
m/s,
um
ponto
material
possui
aceleração
escalar
constante e igual a 4,0 m/s
2
. Considerando que o ponto material se desloque em uma trajetória horizontal e retilínea, determine:
a) qual a posição do ponto material no instante t = 2,0 s.
b) a equação horária da velocidade,c) em que instante o corpo muda o seu sentido.
P13.
(UFSC
-
1988)
Um
móvel
descreve
um
movimento
retilíneo
uniformemente
acelerado
numa
trajetória
em
linha
reta
e
suas
posições
variam
no
tempo
de
acordo
com
a
equação
s
=
20
+
2.t
+
2.t
2
onde
s
é
medido
em
metros
e
t
em
segundos.
Determine
a
velocidade
do
móvel
quando
o
tempo t for igual a 10 s.
P14.
(FAU-USP)
Partindo
do
repouso
no
instante
t
=
0,
um
ponto
material
possui
aceleração
escalar
constante
e
igual
a
2,0
m/s
2
.
Qual
a
distância
percorrida entre os instantes t
1
= 1,0 s e t
2
= 2,0 s?

P15.
(UERJ
2014)
O
cérebro
humano
demora
cerca
de
0,36
segundos
para
responder
a
um
estímulo.
Por
exemplo,
se
um
motorista
decide
parar
o carro, levará no mínimo esse tempo de resposta para acionar o freio.
Determine
a
distância
que
um
carro
a
100
km/h
percorre
durante
o
tempo
de
resposta
do
motorista
e
calcule
a
aceleração
média
imposta
ao
carro se ele para totalmente em 5 segundos.
2.5.h Testes propostos
T1.
(Unicamp
2024)
Uma
das
etapas
mais
difíceis
de
um
voo
espacial
tripulado
é
a
reentrada
na
atmosfera
terrestre.
Ao
reencontrar
as
camadas
mais
altas
da
atmosfera,
a
nave
sofre
forte
desaceleração
e
sua
temperatura
externa
atinge
milhares
de
graus
Celsius.
Caso
a
reentrada
não
ocorra
dentro
das
condições
apropriadas,
há
risco
de
graves
danos
à
nave,
inclusive
de
explosão,
e
até
mesmo
risco
de
ela
ser
lançada
de
volta
ao espaço.
Logo
ao
reentrar
na
atmosfera
terrestre,
uma
cápsula
espacial
passa
a
descrever,
durante
certo
tempo,
um
movimento
retilíneo
uniformemente
variado
em
que
ela
é
freada
com
aceleração
a
=
-
5m/s
2
.
Se
no
início
dessa
etapa
(t
=
0)
do
movimento
a
velocidade
da
cápsula
é
V
0
=
7
000
m/s,
qual é a distância percorrida até o tempo t = 200 s?
a) 1300 km. b) 1400 km. c) 1500 km. d) 4900 km.
T2.
(Unicamp
2023)
O
balonismo,
um
esporte
aeronáutico
com
adeptos
em
todo
o
mundo,
oferece
um
belo
espetáculo
para
os
observadores
no
solo.
Um
maçarico
é
usado
para
aquecer
o
ar
no
interior
do
balão,
o
que
faz
variar
a
densidade
do
ar,
permitindo
o
controle
do
movimento
de
subida e descida do balão.
Um
balão,
inicialmente
em
repouso
no
solo,
decola
e
sobe
em
movimento
uniformemente
variado.
Se
o
balão
atinge
a
altura
h
=
80
m
após
um
tempo t = 40 s, conclui-se que a aceleração vertical do balão nesse movimento é igual a
a) 2,0 m/s
2
b) 4,0 m/s
2
c) 0,05 m/s
2
d) 0,1 m/s
2
T3.
(Fmc
2021)
Dois
atletas
A
e
B
correm
ao
longo
de
linhas
retas
paralelas.
Suas
respectivas
posições
e
nessas
linhas
variam
no
tempo
da
seguinte
forma:
X
A
(t)
=
c.t
e
X
B
(t)
=
d
+
b.t
- a.t
2
/2
onde
d=
5
m,
b
=
10
m/s,
a
=
2m/s
2
e
c
=
6
m/s.
A
partir
do
instante
inicial
t
=
0
s
o
tempo
necessário para que os atletas atinjam velocidades idênticas é de:
a) 2 s b) 4 s c) 5 s d) 6 s e) 8 s
T4.
(Famerp
2021)
O
sangue
percorre
as
grandes
artérias
do
corpo
humano
com
velocidade
aproximada
de
30,00
cm/s
e
os
vasos
capilares
com
velocidade
de
0,05
cm/s.
Supondo
que
o
intervalo
de
tempo
para
certa
massa
de
sangue
ir
de
uma
grande
artéria
até
um
vaso
capilar
seja
de
30
s essa massa de sangue será submetida, nesse deslocamento, a uma aceleração média, em valor absoluto, de aproximadamente
a) 0,05 m/s
2
b) 0,01 m/s
2
c) 0,10 m/s
2
d) 0,25 m/s
2
e) 0,50 m/s
2
T5.
(Ueg
2021)
Uma
partícula
sai
de
um
ponto
A
com
velocidade
inicial
V
0
=
1
m/s
e
desliza
em
linha
reta
até
chegar
em
um
ponto
B,
dez
segundos
depois,
com
velocidade
V
=
5
m/s.
Sabendo-se
que
a
equação
da
velocidade
dessa
partícula
em
função
do
tempo
t
é
V
=
V
0
+
t
a
aceleração do movimento é
a) 0,2 m/s
2
b) 0,4 m/s
2
c) 0,6 m/s
2
d) 0,8 m/s
2
e) 1,0 m/s
2
T6.
(Acafe
2018)
A
Física
é
a
ciência
responsável
pelos
fenômenos
que
acontecem
ao
nosso
redor,
sendo
que
a
relação
com
a
Matemática
se
traduz
em
expressões
algébricas
ou
fórmulas
matemáticas,
que
embasam
os
fundamentos
teóricos.
Em
um
M.R.U.V.
para
um
determinado
móvel a velocidade do mesmo é descrita pela equação V = 50 – 10.t (em unidades do SI).
Neste caso, a alternativa correta que apresenta o instante, em s que o móvel inverte o sentido do movimento é:
a) 0,5 b) 5,0 c) 1,0 d) 0,2
T7.
(Unesp
2018)
Um
foguete
lançador
de
satélites,
partindo
do
repouso,
atinge
a
velocidade
de
5400
km/h
após
50
segundos.
Supondo
que
esse foguete se desloque em trajetória retilínea, sua aceleração escalar média é de
a) 30 m/s
2
b) 150 m/s
2
c) 388 m/s
2
d) 108 m/s
2
e) 54 m/s
2
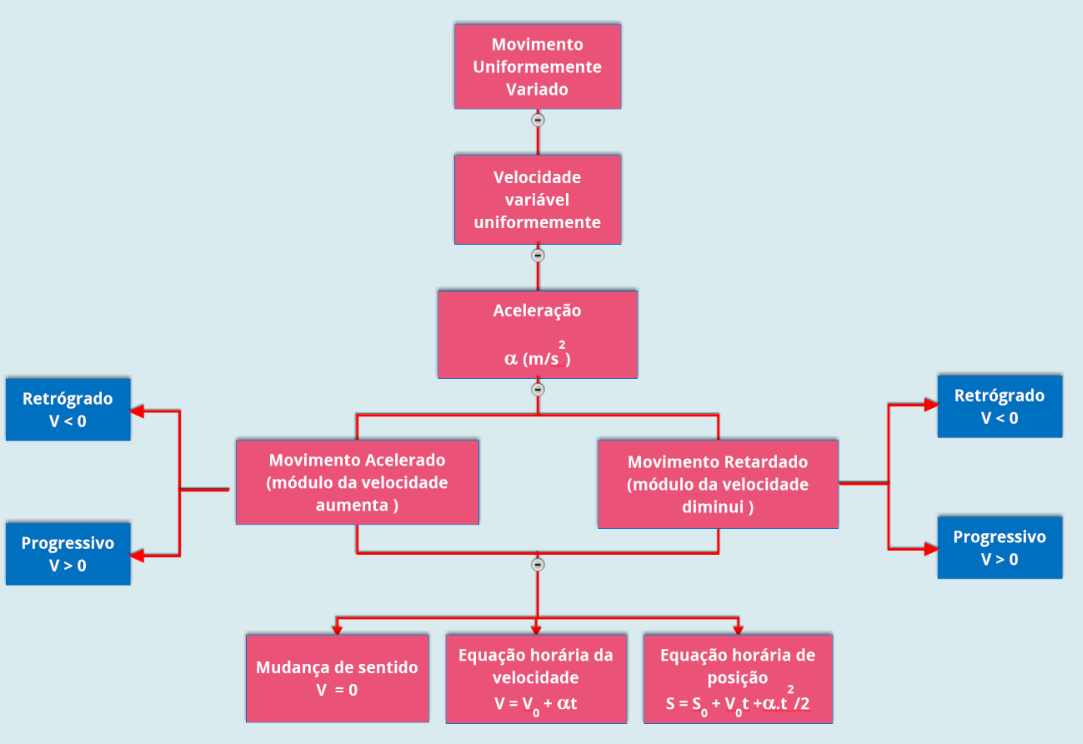
2.5.i Mapa conceitual
Este
mapa
conceitual
apresenta
uma
visão
geral
dos
exemplos
e
conceitos
vistos
nesta
página,
ele
se
apresenta
na
forma
de
um
conjunto
de
proposições
interconectadas.
O
significado
de
qualquer
conceito
é
a
soma
de
todas
as
ligações
que
contêm
o
conceito.
Para
"ler"
o
mapa
conceitual, comece do Movimento Uniformemnte Variado, e vá até os itens mais específicos e os exemplos nas partes mais externas.
Procure fazer o teu mapa conceitual, vai te ajudar a organizar os conceitos desta lição.

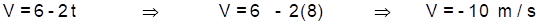
ciencia-cultura.com
MRUV - eq. Torricelli
MRUV - aceleração



As
equações
horárias
do
MRUV
são
ferramentas
fundamentais
na
Mecânica,
especialmente
na
cinemática,
pois
permitem
descrever
de
forma
precisa e matemática o movimento de um corpo que se move em linha reta e com aceleração constante.
Por que são importantes?
Previsibilidade:
Com
as
equações
horárias,
é
possível
prever
a
posição,
a
velocidade
de
um
corpo
em
qualquer
instante
de
tempo,
desde
que
se
conheçam
os
valores
iniciais
de
posição,
velocidade
e
a
aceleração.
Este
conceito
em
possibilitar
o
que
pode
ocorrer
com o movimento, é crucial em diversas áreas física.
Análise
de
movimento:
Ao
analisar
as
equações,
podemos
obter
informações
importantes
sobre
o
movimento,
como
a
direção
(se
o
movimento
é
acelerado
ou
retardado),
o
sentido
(se
é
progressivo
ou
retrógrado)
e
a
distância
percorrida
em
um
determinado
intervalo de tempo.
Resolução
de
problemas:
As
equações
horárias
são
a
base
para
a
resolução
de
uma
grande
variedade
de
problemas
envolvendo
movimento, desde a queda livre de um objeto até o lançamento de projéteis.
Quais são as principais
equações horárias
do MRUV?
As equações horárias do MRUV são:
Posição (S):
S = S
₀
+ V
₀
t + (
a
t²)/2
Velocidade
(V): V = V
₀
+
a
t







Alternativa B


Alternativa B










O problema nos fornece a equação horária da velocidade: v = 4 + 3 (SI) Por meio desta equação poderemos responder o que o exercício nos pede. a) e b) A velocidade inicial e a aceleração do corpo pode ser obtida comparando as equações.






Inicialmente vamos organizar os dados fornecidos pelo problema. A velocidade possui unidades de medida diferente da aceleração. Devemos transformar km/h para m/s.
Note que o valor da aceleração, é dado da seguinte forma: "à razão de 4 m/s em cada segundo"



a) Inicialmente vamos organizar os dados fornecidos pelo problema, note que a velocidade está em km/h, enquanto o valor da aceleração em m/s. Vamos utilizar o sistema internacional, que utiliza o metro e segundo.



O problema nos fornece a equação horária: V= 4 - 3t (SI). Por meio desta equação podemos responder aos itens a e b.


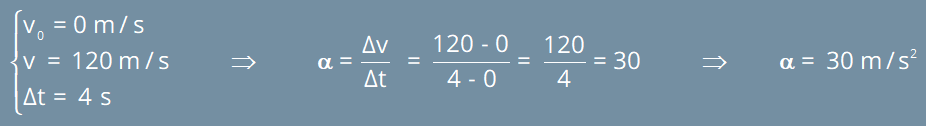
Como colaborar.
Este
site
não
possui
finan-
ciamento algum.
A
forma
que
eu
encontrei
para
arrecadar
fundos,
é
ofertar
a
compra
do
livro
indicado na figura abaixo.
Testes
da
Fuvest
com
reso-
lução comentada.















