Na situação descrita, o módulo do vetor deslocamento (d) do cidadão,da praça até
a festa, corresponde a menor distância entre estes dois locais.
Como mostra o cálculo da hipotenusa, d = 5 km.
© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física
Cinemática
Capítulo 3.1 – Cinemática vetorial
3.1 Introdução.
No
video
ao
lado,
nos
mostra
uma
simulação
do
movimento
da
Estação
espacial
Internacional
realizando
um
movimento
circular
ao
redor
da
Terra,
onde
leva
91,34
minutos
para
completar
uma
volta
com
uma
velocidade
de
7,69
km/s.
Você
pode
utlizar
a
simulação
para
aprender
mais, acessando
PHET - Gravidade e órbitas.
3.1.a Distância e deslocamento
Distância
e
deslocamento
são
duas
grandezas
que,
à
primeira
vista,
podem
parecer
semelhantes,
mas
na
Física
possuem
significados
distintos.
•
Distância
é
uma
grandeza
escalar
que
indica
quanto
um
corpo
percorreu
ao
longo
de
um
trajeto,
independentemente
da
direção ou sentido.
•
Deslocamento
,
por
outro
lado,
é
uma
grandeza
vetorial
que
representa
a
variação
da
posição
de
um
corpo
—
ou
seja,
depende
da
posição
inicial
e
final,
bem
como
da
direção
e
sentido
do movimento.
Vamos
analisar
um
exemplo:
imagine
uma
pessoa
que
inicia
seu
trajeto
em
um
cruzamento
de
ruas
,
indicado
como
o
ponto
A
(conforme
mostra
a
figura
ao
lado).
Essa
pessoa
caminha
por
diversas
ruas
e,
ao
final
do percurso, retorna ao ponto de partida, também o ponto A.
A
distância percorrida
é a soma de todos os trechos caminhados:
d = 200 m + 400 m + 100 m + 160 m + 100 m + 240 m = 1 200 m
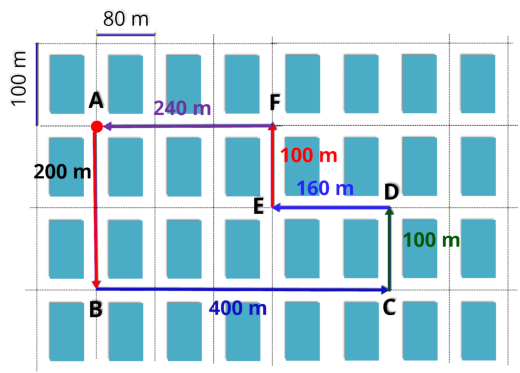
Portanto, a pessoa percorreu uma
distância total de 1 200 metros.
Contudo,
como
ela
retornou
ao
ponto
de
origem
,
sua
posição
final
é
igual
à
posição
inicial.
Isso
significa
que
não
houve
mudança
de
posição
— logo, o
deslocamento é igual a zero
:
•
Deslocmento = 0 m
Esse
exemplo
deixa
claro
que
distância
e
deslocamento
são
grandezas
diferentes
.
A
distância
mede
o
caminho
total
percorrido.
O
deslocamento mede a mudança efetiva de posição.
•
A
distância
mede o caminho total percorrido.
•
O
deslocamento
mede
a mudança efetiva de posição.
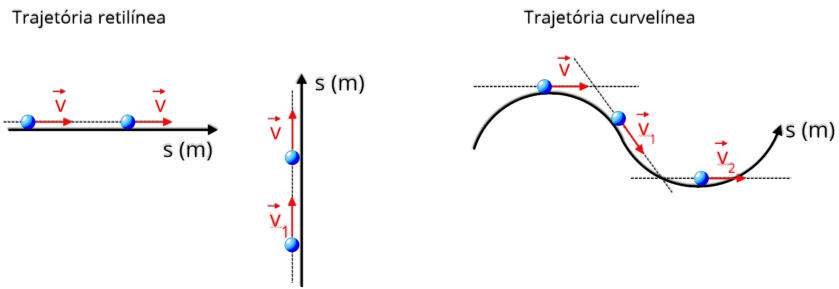
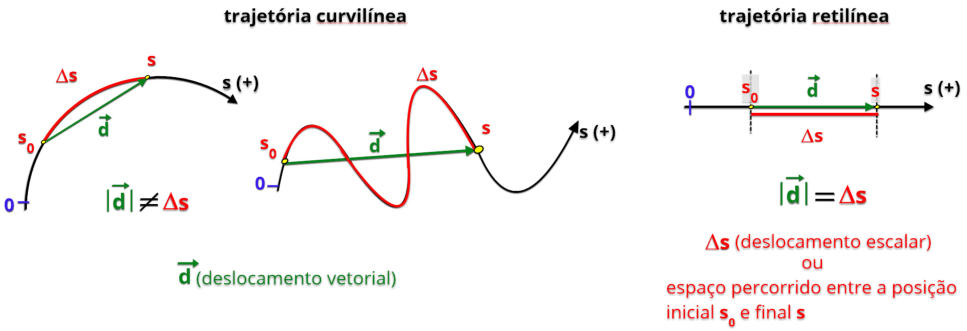
Em
trajetórias
retilíneas
podemos
afirmar
que
o
módulo
do
deslocamento
possui
o
mesmo
valor
da
distância
percorrida
.
O
mesmo
não
ocorre em trajetórias curvelíneas.
3.1.b Exercícios Resolvidos.
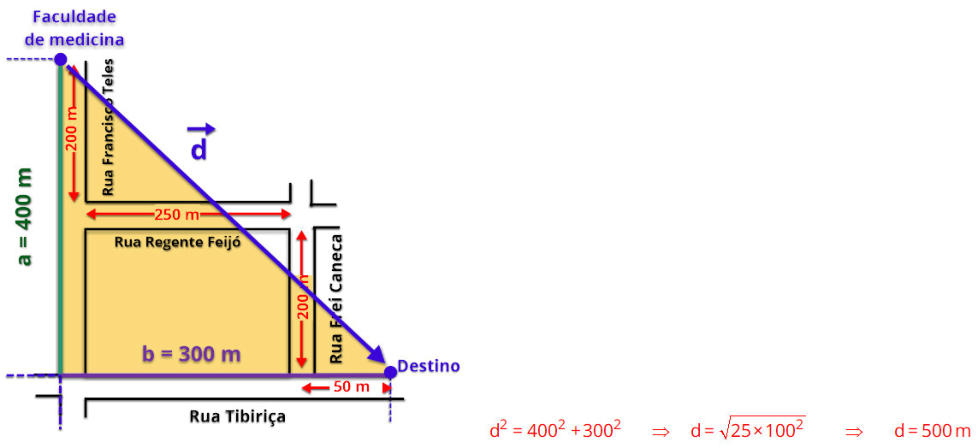
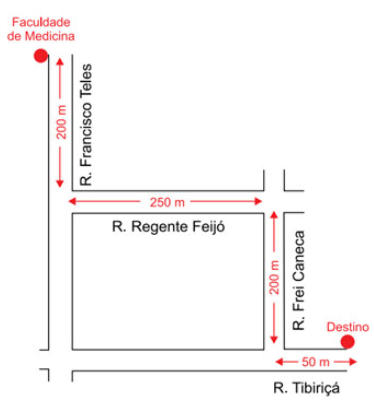
R1. (Fmj 2023) Uma pessoa saiu da Faculdade de Medicina, caminhou 200 m pela rua Francisco Teles, entrou à esquerda na rua Regente Feijó,
onde caminhou por 250 m, entrou à direita na rua Frei Caneca, caminhou 200 m por ela e, finalmente, entrou à esquerda na rua Tibiriçá, por
onde caminhou mais 50 m até o seu destino.
Considerando que essas ruas são perpendiculares entre si, o vetor que representa o
deslocamento dessa pessoa entre a Faculdade de Medicina e o seu destino tem módulo
igual a
a) 500 m.
b) 550 m.
c) 600 m.
d) 650 m.
e) 700 m.
Resolução:
3.1.c
Velocidade vetorial
.
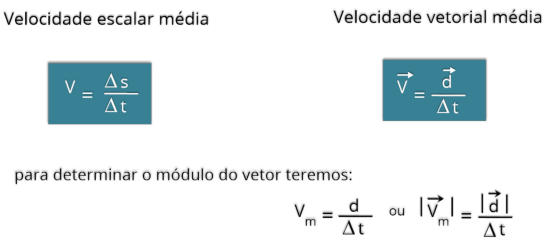
A velocidade vetorial é uma grandeza vetorial que descreve o movimento de um corpo com base em três características fundamentais:
✅ Características da Velocidade Vetorial:
•
Módulo (intensidade):
É o valor numérico da velocidade com sua unidade, como m/s (metros por segundo) ou km/h (quilômetros por hora). Indica quão rápido o
corpo se desloca.
•
Direção:
Corresponde à linha de ação do movimento (horizontal, vertical, inclinada, etc.). A direção da velocidade vetorial está associada à
trajetória do objeto.
•
Sentido:
Indica para onde o corpo se move ao longo da direção. Por exemplo, pode ser da esquerda para a direita, de cima para baixo, para o
norte, etc.
Se o movimento ocorre no mesmo sentido da trajetória, considera-se positivo; se for no sentido oposto, negativo.
✅
Velocidade Média e Velocidade Instantânea:
•
Velocidade média:
É o deslocamento total de um objeto dividido pelo tempo total gasto. Ela dá uma visão geral do movimento.
•
Velocidade
instantânea:
Esta
é
a
velocidade
de
um
objeto
em
um
momento
específico
no
tempo.
Ela
pode
mudar
conforme
o
objeto
acelera ou desacelera.
✅
Comportamento do Vetor Velocidade em Diferentes Trajetórias
A seguir, observe como a direção e o sentido do vetor velocidade se comportam em diferentes tipos de trajetórias:
•
Trajetória retilínea: O vetor velocidade mantém direção constante.
•
Trajetória curva: O vetor velocidade muda de direção continuamente, sempre tangente à curva em cada ponto da trajetória.
Para determinar o módulo do vetor deslocamento, o que ocorre na maioria das
vezes, pode ser em um mapa ou quadriculado ou algo semelhante, o resultado
acaba sendo a formação de um triângulo retângulo. É comum que o vetor
deslocamento acaba sendo a hipotenusa do triângulo retângulo. Quanto aos lados
do triângulo a e b podem ser determinados pelas distâncias fornecidas na figura.
Na vertical teremos dois quarteirões de 200 m cada, formando um lado onde a =
400 m, a base do triângulo é a soma de um quarteirão de 250 m com um pedaço
de 50 m, sendo b = 300 m.
Utilizando Pitágoras teremos:
Inicialmente
devemos
traçar
o
vetor
resultante
da
caminhada,
que
tem
início
na
Faculdade
de
Medicina
e
termina
no
Destino,
como
indica
a
figura
ao
lado.
Este
vetor
resultante
o
denominamos
de
vetor
deslcamento,
que
indica
o
deslocamento entre as duas posições, a faculdadde de Medicina e seu destino.
T4.
(Insper
2019)
Existem
cidades
no
mundo
cujo
traçado
visto
de
cima
assemelha-se
a
um
tabuleiro
de
xadrez.
Considere
um
ciclista
trafegando
por
uma
dessas
cidades,
percorrendo,
inicialmente,
2,0
km
no
sentido
leste,
seguindo
por
mais
3,0
km
no
sentido
norte.
A
seguir,
ele
passa
a
se
movimentar
no
sentido
leste,
percorrendo,
novamente,
1,0
km
e
finalizando
com
mais
3,0
km
no
sentido
norte.
Todo
esse
percurso
é
realizado
em
18
minutos.
A
relação
percentual
entre
o
módulo
da
velocidade
vetorial
média
desenvolvida
pelo
ciclista
e
a
respectiva
velocidade
escalar
média deve ter sido mais próxima de
a) 72 % b) 74 % c) 77 % d) 76 % e) 70 %
R2.
(Uel
2018)
Em
uma
brincadeira
de
caça
ao
tesouro,
o
mapa
diz
que
para
chegar
ao
local
onde
a
arca
de
ouro
está
enterrada,
deve-se,
primeiramente,
dar
dez
passos
na
direção
norte,
depois
doze
passos
para
a
direção
leste,
em
seguida,
sete
passos
para
o
sul,
e
finalmente
oito
passos para oeste.
A partir dessas informações, responda aos itens a seguir.
a) Desenhe a trajetória descrita no mapa, usando um diagrama de vetores.
b) Se um caçador de tesouro caminhasse em linha reta, desde o ponto de partida até
o ponto de chegada, quantos passos ele daria?
Justifique sua resposta, apresentando os cálculos envolvidos na resolução deste item.
Resolução:
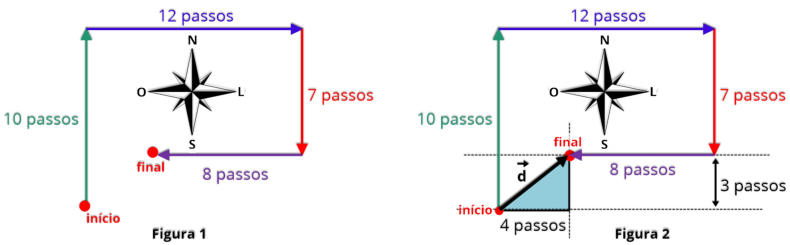
b)
A
frase
“caminhasse
em
linha
reta
do
ponto
de
partida
até
o
ponto
de
chegada”
nos
indica
que
devemos
calcular
o
vetor
deslocamento
que
tem
origem no “início” e termina na posição final como indica a Figura 2.
Para
determinar
em
passos
qual
seria
o
módulo
do
vetor
deslocamento,
perceba
que
é
possivel
montar
um
triângulo
retângulo
onde
o
deslocamento
é
a
hipotenusa. Esta forma nos permite constatar que um lado do triângulo vale 4 passos, e o outro três passos. Aplicando pitágoras teremos:
Vamos estudar o movimento retilíneo uniforme e o uniformemente variado. Como ficam estes movimento considerando a velocidade um vetor?
3.1.f Velocidade no movimento curvelíneo.
Para
determinar
a
velocidade
vetorial
em
um
movimento,
você
precisa
conhecer
o
vetor
deslocamento
e
o
intervalo
de
tempo
em
que
o
deslocamento ocorreu.
Para calcular a velocidade média vetorial, temos:
3.1.d Exercícios Resolvidos
R3.
(Mackenzie
–
SP)
A
figura
em
escala
mostra
os
vetores
deslocamento
de
uma
formiga,
que,
saindo
do
ponto
A,
chegou
ao
ponto
B,
após
3
minutos
e
20
s.
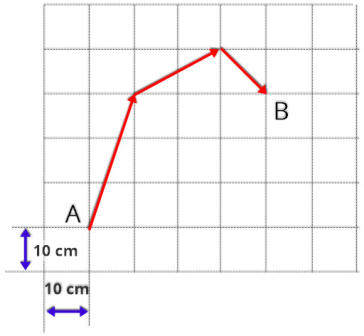
O
módulo
do
vetor
velocidade
média do movimento da formiga, nesse trajeto, foi de:
a) 0,15 cm/s b) 0,20 cm/s c) 0,25 cm/s d) 0,30 cm/s e) 0,40 cm/s
Resolução.
Para
determinar
a
velocidade
vetorial
em
um
movimento,
é
necessário
conhecer
o
vetor
deslocamento
e o
intervalo de tempo
em que o deslocamento ocorreu.
O
Vetor
deslocamento,
pode
ser
obtido
na
figura
fornecida
pelo
exercício,
ele
inicia
na
posição
A
e
termina
na
posição
final
B
.
Perceba
que
através
do
quadriculado
é
possivel
determinar
o
módulo
do
vetor
deslocamento.
Nestes
casos
o
vetor
deslocamento
acaba
sendo
a
hipotenusa
de
um
triângulo
retângulo.
Como cada quadrado vale 10 cm, assim os lados do triângulo valem 40 cm e 30 cm.
O
Intervalo
de
tempo
que
o
objeto
levou
para
se
mover
da
sua
posição
inicial
para
a
sua
posição
final, é
D
t = 3 min e 20 s = 3(60 s) + 20 s = 200 s
D
t = 200 s
d = 50 cm
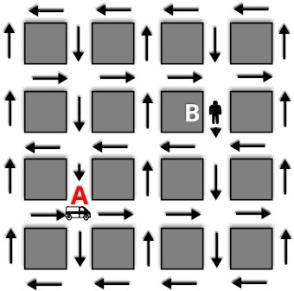
R4.
(Unicamp
1996)
A
figura
a
seguir
representa
um
mapa
da
cidade
de
Vectoria
o
qual
indica
a
direção
das
mãos
do
tráfego.
Devido
ao
congestionamento,
os
veículos
trafegam
com
a
velocidade
média
de
18
km/h.
Cada
quadra
desta
cidade
mede
200
m
por
200
m
(do
centro
de
uma
rua
ao
centro
de
outra
rua).
Uma
ambulância
localizada
em
A
precisa
pegar
um
doente
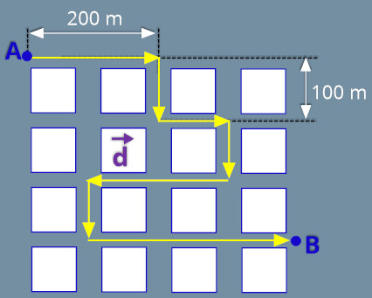
localizado bem no meio da quadra em B, sem andar na contramão.
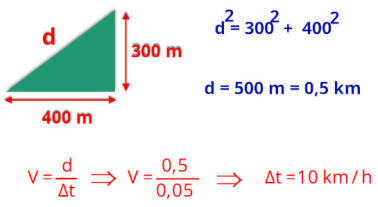
a) Qual o menor tempo gasto (em minutos) no percurso de A para B?
b) Qual é o módulo do vetor velocidade média (em km/h) entre os pontos A e B?
Resolução.
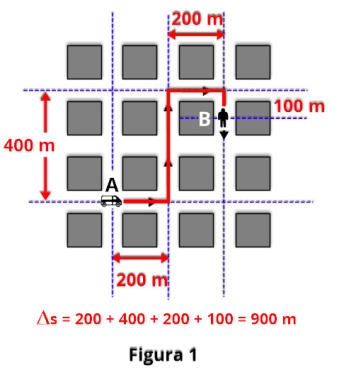
a)
Para
determinar
o
tempo
do
percurso
estamos
falando
do
espaço
percorrido,
como
mostra
a
Figura 1.
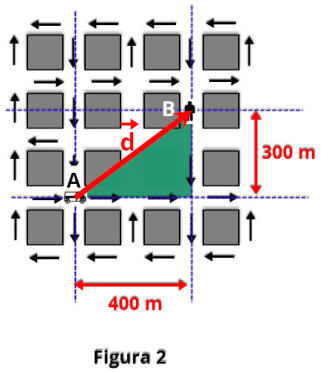
b)
O
Vetor
deslocamento,
pode
ser
obtido
na
figura
fornecida
pelo
exercício,
ele
inicia
na
posição
A
e
termina na posição final
B,
como mostra a Figura 2.
Perceba
que
através
do
quadriculado
é
possivel
determinar
o
módulo
do
vetor
deslocamento.
Nestes
casos o vetor deslocamento acaba sendo a hipotenusa de um triângulo retângulo.
Como cada quadrado vale 200 m, assim os lados do triângulo valem 400 m e 300 m.
3.1.e Testes propostos
T1.
(Puccamp
1998)
Num
bairro,
onde
todos
os
quarteirões
são
quadrados
e
as
ruas
paralelas
distam
100
m
uma
da
outra,
um
transeunte
faz
o
percurso
de
P
a
Q
pela
trajetória
representada
no esquema a seguir. O deslocamento vetorial desse transeunte tem módulo, em metros, igual a
a) 300 b) 350 c) 400 d) 500 e) 700
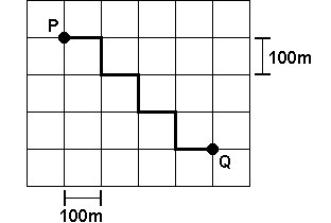
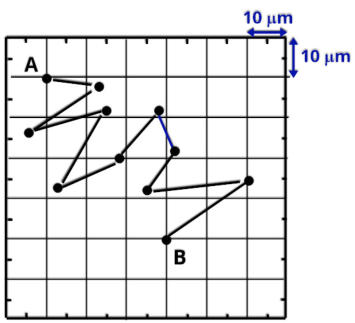
T2. (Unicamp 2015) Movimento browniano é o deslocamento aleatório de partículas
microscópicas suspensas em um fluido, devido às colisões com moléculas do fluido em agitação
térmica.
A figura abaixo mostra a trajetória de uma partícula em movimento browniano em um líquido
após várias colisões. Sabendo-se que os pontos negros correspondem a posições da partícula a
cada 30 s, qual é o módulo da velocidade média desta partícula entre as posições A e B.
Se
amarrarmos
uma
pedra
a
um
pedaço
de
barbante
e
a
colocarmos
para
girar,
observaremos
um
movimento
semelhante
ao
representado
na
figura
ao
lado.
Enquanto
o
barbante
não
se
romper, a pedra descreverá uma trajetória circular.
Nesse
tipo
de
movimento,
o
vetor
velocidade
está
em
constante
mudança
de
direção.
Para
simplificar
a
análise,
vamos
considerar
que
o
módulo
da
velocidade
vetorial
permanece constante durante o movimento.
É
importante
destacar
que,
em
movimentos
curvilíneos
—
especialmente
nos
circulares
—
qualquer
alteração
em
pelo
menos
uma
das
características
do
vetor
velocidade
(módulo,
direção
ou
sentido)
representa
uma
variação
dessa
grandeza vetorial.
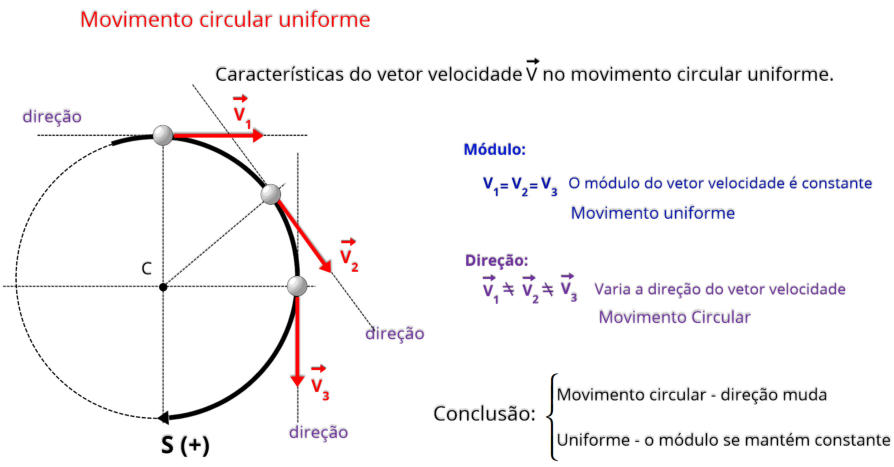
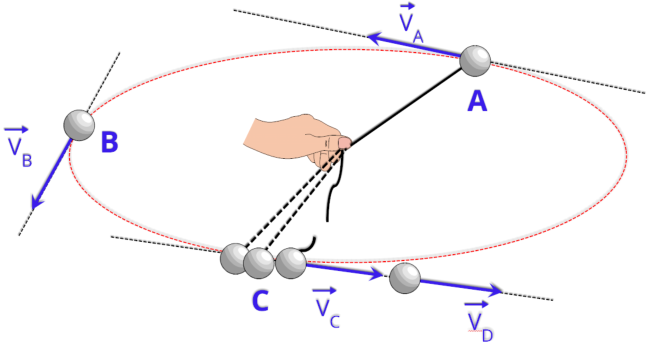
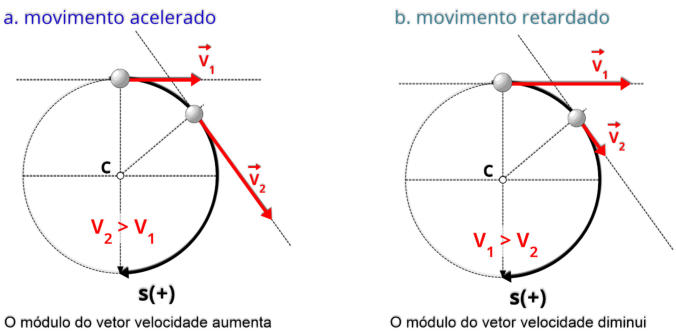
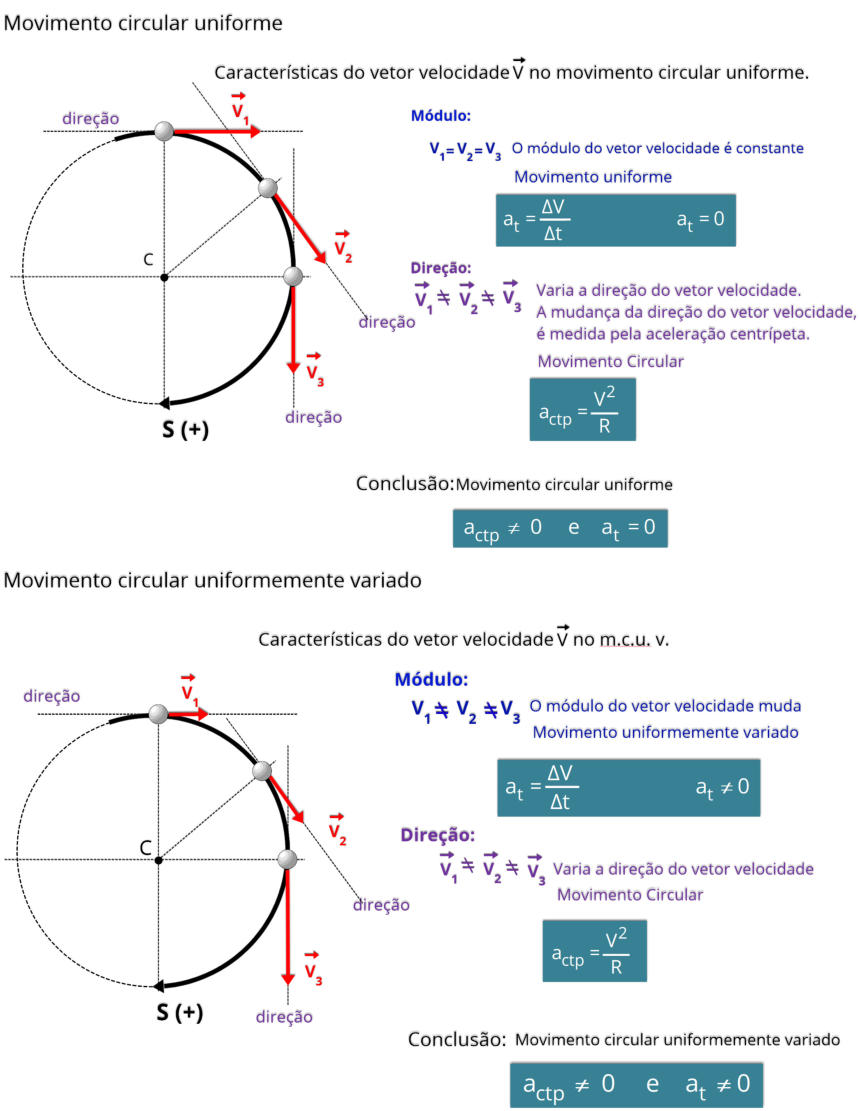
No movimento circular uniforme (MCU), o vetor velocidade de um corpo muda continuamente de direção, embora seu módulo permaneça
constante.
Veja a seguir uma análise desse comportamento:
Módulo constante: O corpo se desloca ao redor da circunferência com velocidade constante, ou seja, o valor (módulo) do vetor velocidade
não se altera ao longo do tempo.
Mudança de direção: Apesar de o módulo ser constante, a direção do vetor velocidade varia constantemente, pois o corpo está sempre
mudando de posição ao longo da curva.
Direção tangencial: Em qualquer ponto da trajetória, o vetor velocidade é tangente à circunferência. Isso significa que ele aponta na direção
do movimento naquele instante, conforme ilustrado na figura.
Retomando o exemplo da pedra amarrada a um barbante: enquanto o barbante estiver preso, a pedra mantém sua trajetória circular. No
entanto, se o barbante se romper, a pedra será lançada na direção tangente à circunferência naquele ponto — ou seja, seguirá o caminho
indicado pelo vetor velocidade no instante da ruptura.
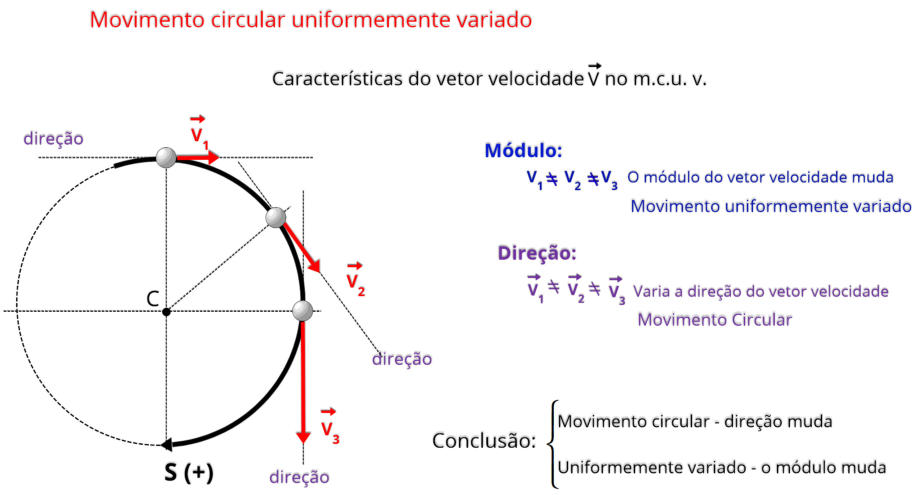
No movimento circular uniformemente variado, o vetor velocidade sofre variações na direção e no módulo.
Aqui está uma análise de como o vetor velocidade se comporta:
Mudando de Direção: Conforme o objeto se move ao redor do círculo, sua direção de movimento muda, sempre apontando na direção em
que o objeto está se movendo.
Mudança do módulo: A velocidade do objeto está aumentando ou diminuindo a uma taxa constante. Isso significa que o módulo do vetor
de velocidade também está mudando de forma constante.
Velocidade crescente: se o objeto estiver acelerando, o módulo do vetor velocidade aumentará.
Velocidade decrescente: se o objeto estiver desacelerando, o módulo do vetor velocidade diminuirá.
Concluímos que essa mudança constante na direção e no módulo do vetor velocidade é o que faz com que o objeto se mova em um círculo
com uma velocidade variável.
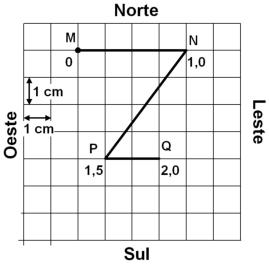
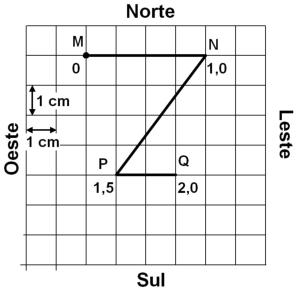
T5.
(UCSal-BA
-
1987)
Uma
partícula
percorreu
a
trajetória
MNPQ,
representada
na
figura
ao
lado. Os instantes de passagem pelos diferentes pontos estão anotados em segundos.
a)A
velocidade
vetorial
média
da
partícula
durante
todo
o
percurso
tem
módulo,
em
cm/s,
igual a:
a) 6,0
b) 5,5
c) 4,5
d) 2,5
e) 2,0
3.1.g Aceleração na cinemática vetorial
Para
entendermos
o
conceito
de
aceleração,
é
fundamental
lembrar
que
o
vetor
velocidade possui duas características principais:
módulo e direção
.
No
movimento
circular,
a
variação
do
módulo
da
velocidade
é
chamada
de
aceleração
tangencial
,
enquanto
a
aceleração
centrípeta
está
relacionada
à
mudança
na
direção
do
vetor
velocidade.
O
vetor
velocidade,
nesse
tipo
de
movimento,
é
sempre
tangente
à
trajetória
no
ponto
em
que
o
corpo
se
encontra.
Podemos
visualizar
isso
na
figura
ao
lado:
o
balde
gira
preso
por
uma
corda
ao
centro
da
trajetória.
O
movimento
circular
só
ocorre
enquanto
a
corda
permanecer
intacta.
Caso
ela
se
rompa,
o
balde
seguirá
em
linha
reta
na
direção
tangente
à
trajetória naquele instante — ou seja, seguirá o vetor velocidade.
A
aceleração
tangencial
indica
como
o
módulo
da
velocidade
varia
ao
longo
do
tempo,
ou
seja,
se
o
corpo
está
acelerando
ou
desacelerando.
Esse
conceito
é
essencial
para
compreender
o
movimento
de
corpos
que
percorrem
trajetórias
curvilíneas
não
uniformes
—
em
que
a
velocidade não se mantém constante
.
Veja, a seguir, dois exemplos que ilustram diferentes situações no movimento circular.
3.1.h Testes propostos
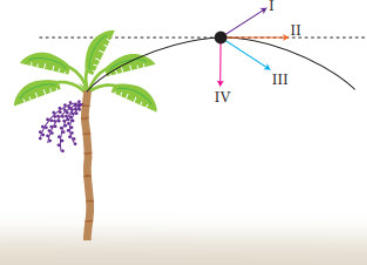
T3.
(Uerj
2024)
Durante
uma
ventania,
uma
árvore
sofreu
certa
inclinação
e,
depois,
retornou
à
posição
inicial.
Nesse
processo,
um
de
seus
frutos
foi
projetado
e
submetido
à
ação
exclusiva
da
gravidade,
descrevendo
um
arco
de
parábola.
Observe
no
esquema
a
trajetória
do
fruto
e
as
setas
I,
II,
III
e
IV,
que
representam
possíveis
vetores
de
velocidade
resultante na altura máxima.
Sabe-se que a altura máxima é alcançada pelo fruto alguns instantes após seu lançamento.
Nesse caso, o vetor velocidade resultante do fruto é representado pela seguinte seta:
a) I b) II c) III d) IV
T7.
(Mackenzie
2012)
Um
avião,
após
deslocar-se
120
km
para
nordeste
(NE),
desloca-se
160
km
para
sudeste
(SE).
Sendo
um
quarto
de
hora,
o
tempo total dessa viagem, o módulo da velocidade vetorial média do avião, nesse tempo, foi de
a) 320 km/h b) 480 km/h c) 540 km/h d) 640 km/h e) 800 km/h
T8.
(Pucpr
2004)
Um
ônibus
percorre
em
30
minutos
as
ruas
de
um
bairro,
de
A
até
B,
como
mostra a figura ao lado.
Considerando
a
distância
entre
duas
ruas
paralelas
consecutivas
igual
a
100
m,
analise
as
afirmações:
I. A velocidade vetorial média nesse percurso tem módulo 1 km/h.
II. O ônibus percorre 1500 m entre os pontos A e B.
III. O módulo do vetor deslocamento é 500 m.
IV. A velocidade vetorial média do ônibus entre A e B tem módulo 3 km/h.
Estão corretas:
a) I e III. b) I e IV. c) III e IV. d) I e II. e) II e III.
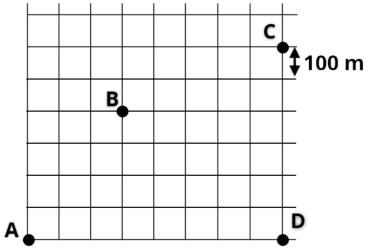
T9.
(Ufc
2003)
A
figura
adiante
mostra
o
mapa
de
uma
cidade
em
que
as
ruas
retilíneas
se
cruzam
perpendicularmente
e
cada
quarteirão
mede
100
m.
Você
caminha
pelas
ruas
a
partir
de
sua
casa,
na
esquina
A,
até
a
casa
de
sua
avó,
na
esquina
B.
Dali
segue
até
sua
escola,
situada
na
esquina
C.
A
menor
distância
que
você
caminha
e
a
distância
em
linha
reta entre sua casa e a escola são, respectivamente:
a) 1800 m e 1400 m.
b) 1600 m e 1200 m.
c) 1400 m e 1000 m.
d) 1200 m e 800 m.
e) 1000 m e 600 m.
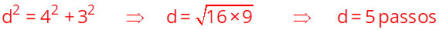
T6.
(UCSal-BA
-
1987)
Uma
partícula
percorreu
a
trajetória
MNPQ,
representada
na
figura
ao
lado.
Os
instantes
de
passagem
pelos
diferentes
pontos
estão
anotados
em
segundos.
A
velocidade
vetorial
média
da
partícula
durante
todo
o
percurso
tem
módulo,
em
cm/s,
igual
a:
a) 6,0 b) 5,5 c) 4,5 d) 2,5; e) 2,0
T10.
(ifsul
2016)
Uma
partícula
de
certa
massa
movimenta-se
sobre
um
plano
horizontal,
realizando
meia
volta
em
uma
circunferência
de
raio
5,00m Considerando π = 3,14, a distância percorrida e o módulo do vetor deslocamento são, respectivamente, iguais a:
a) 15,7 m e 10,00 m b) 31,4 m e 10,00 m c) 15,70 m e 15,70 m d) 10,00 m e 15,70 m
T
T11.
(Ufpb
2006)
Um
cidadão
está
à
procura
de
uma
festa.
Ele
parte
de
uma
praça,
com
a
informação
de
que
o
endereço
procurado
estaria
situado
a
2
km
ao
norte.
Após
chegar
ao
referido
local,
ele
recebe
nova
informação
de
que
deveria
se
deslocar
4
km
para
o
leste.
Não
encontrando
ainda
o
endereço,
o
cidadão
pede
informação
a
outra
pessoa,
que
diz
estar
a
festa
acontecendo
a
5
km
ao
sul
daquele
ponto.
Seguindo
essa
dica,
ele
finalmente
chega
ao
evento.
Na
situação
descrita,
o
módulo
do
vetor
deslocamento
do
cidadão,
da
praça
até
o
destino
final, é:
a) 11 km b) 7 km c) 5 km d) 4 km e) 3 km
Características do vetor aceleração
A
aceleração
centrípeta
é
um
conceito
fundamental,
especialmente
no
estudo
da
dinâmica
do
movimento
circular.
Ela
é
a
responsável
por
manter um objeto em uma trajetória curva, atuando continuamente no sentido do centro dessa curva.
Neste
momento,
não
entraremos
em
detalhes
aprofundados
sobre
a
aceleração
centrípeta,
pois
retomaremos
esse
tema
quando
abordarmos
a
dinâmica
do
movimento
circular.
Entretanto,
na
figura
abaixo,
apresentamos
uma
situação
que
ilustra
tanto
a
aceleração
centrípeta quanto a aceleração tangencial.
Sobre a aceleração centrípeta, podemos destacar:
•
Direção:
Sempre aponta para o
centro da circunferência
que o objeto percorre.
•
Sentido:
Independente
do
sentido
do
movimento
(horário
ou
anti-horário),
a
aceleração
centrípeta
é
sempre
orientada
para
o
centro
da
trajetória.
•
Módulo:
O
valor
da
aceleração
centrípeta
depende
do
módulo
da
velocidade
do
objeto
e
do
raio
da
curva
,
conforme
já
foi
demonstrado
anteriormente.
•
Perpendicular
à
velocidade:
O
vetor
aceleração
centrípeta
é
sempre
perpendicular
ao
vetor
velocidade
(forma
um
ângulo
de
90°).
Isso
significa que ela
não altera o módulo da velocidade
, mas apenas sua
direção
, mantendo o objeto em sua trajetória circular.
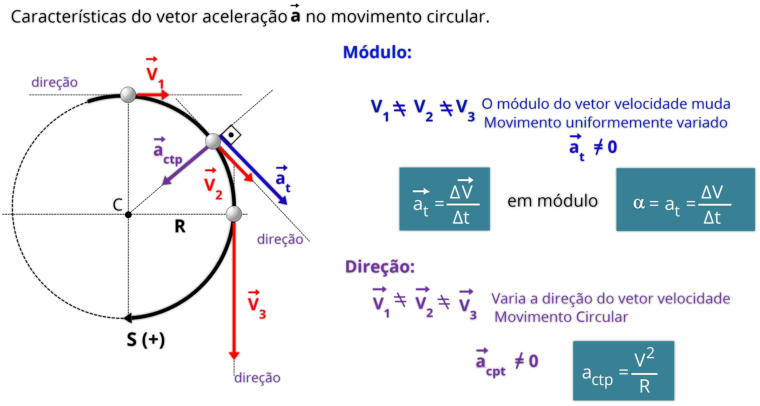
Diferença entre aceleração tangencial e centrípeta:
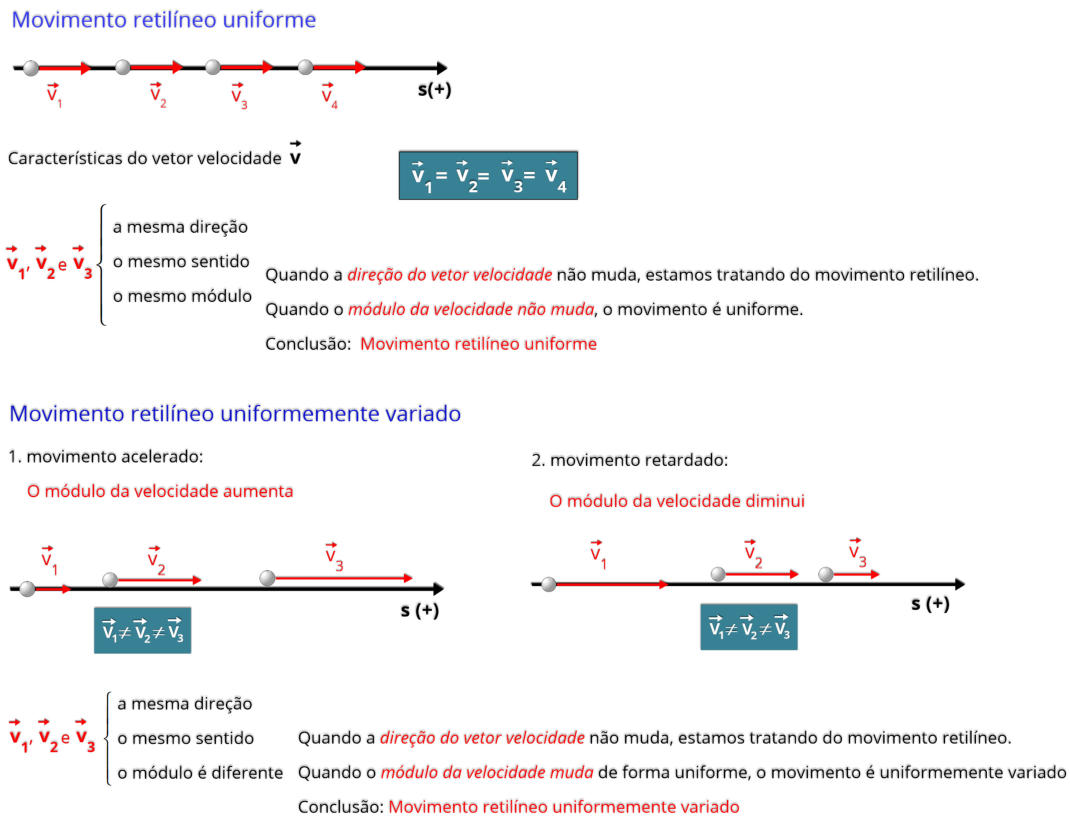
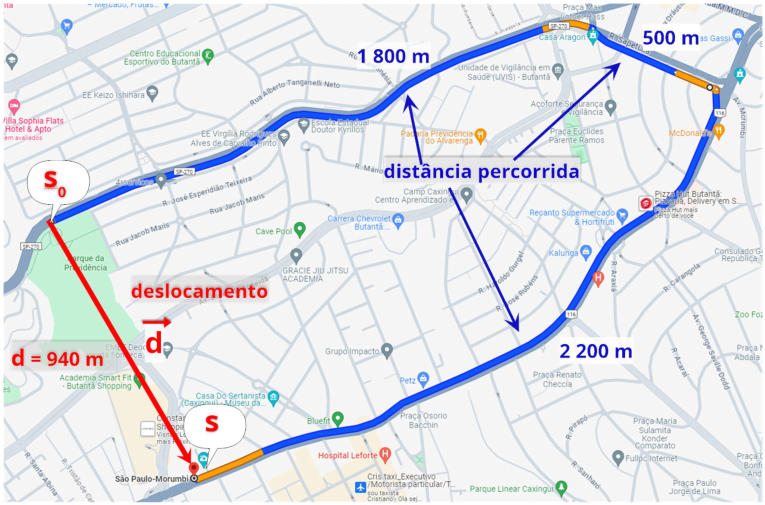
Outro exemplo:
Após uma caminhada no Parque
Previdência (posição inicial, representa-
da por (s₀), João segue pela Rodovia Ra-
poso Tavares, entra na Rua Sapetuba e
depois acessa a Avenida Francisco Mo-
rato, até chegar à sua residência —
indicada no mapa como a posição final
(s).
Vamos determinar a distância
percorrida e o deslocamento de João:
Distância percorrida:
João percorreu os seguintes tre-
chos:
Δs = 1 800 m + 500 m + 2 200 m
Δs = 4 500 m
Portanto, a distância total percor-
rida por João foi de 4 500 metros.
Deslocamento:
Com
base
na
escala
do
mapa
fornecido
pelo
Google
,
foi
possível
medir
a
distância
em
linha
reta
entre
o
ponto
de
partida
(s
₀
)
e
a
posição
final (s).
O resultado foi:
Deslocamento (módulo do vetor deslocamento) = 940 m
Conclusão:
Neste
exemplo,
João
percorreu
uma
distância
total
de
4
500
m
,
mas
seu
deslocamento
foi
de
apenas
940
m
,
pois
essa
é
a
menor
distância
entre
o
ponto
inicial
e
o
ponto
final,
medida
em
linha
reta
e
considerando
a
direção
e
o
sentido
do
movimento
—
exatamente
o
que
caracteriza
um
vetor deslocamento.
Em resumo:
•
Se um
corpo volta ao ponto de partida
, o
deslocamento é zero,
mesmo que a distância tenha sido grande.
•
O
deslocamento
considera
direção e sentido
, enquanto a distância considera apenas o valor total percorrido.
Exemplos de deslocamentos e distâncias percorridas
a) Inicialmente utilizando uma regua,
é possivel obter a figura abaixo, onde
cada
trecho
indica
o
número
de
pas-
sos
dados
na
caça
ao
tesouro
como
mostra
a
Figura
1.
A
rosa
dos
ventos
foi
colocada
no
meio
da
figura
para
orientar
a
direção
e
o
sentido
dos
pas-
sos.
R5. Considere um móvel que percorre a metade de uma pista circular de raio igual a 20,0 m em 10,0 s. Adotando-se √2 como sendo 1,4 e p igual
a 3, determine para este movimento
a) o espaço percorrido pelo móvel;
b) o módulo do deslocamento vetorial do móvel;
c) a velocidade vetorial média do móvel;
d) o módulo da velocidade escalar média do móvel;
Resolução.
Resposta: C
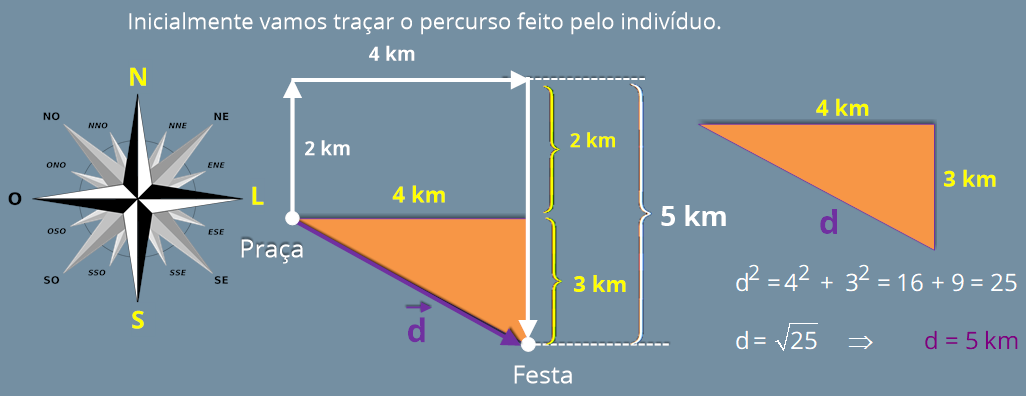
Ao desenharmos o percurso feito pelo indivíduo, caímos em uma situação em que o modulo do vetor deslocamento corresponde a hipotenusa do triângulo.
Na situação descrita, o módulo do vetor deslocamento (d) do cidadão,da praça até
a festa, corresponde a menor distância entre estes dois locais.
Como mostra o cálculo da hipotenusa, d = 5 km.
Na situação descrita, o módulo do vetor deslocamento (d) do cidadão,da praça até
a festa, corresponde a menor distância entre estes dois locais.
Como mostra o cálculo da hipotenusa, d = 5 km.
Resposta: A
Resposta: C
Na figura abaixo calculamos o módulo do vetor deslocamento, que se refere no texto como a "distância em linha reta". e a "menor distância que você caminha" que é a soma de todos os quarteirões que serão percorridos até o ponto C. Como na maioria dos exercícios, o deslocamento é a hipotenusa do triângulo retângulo formado pelos quarteirões da cidade.
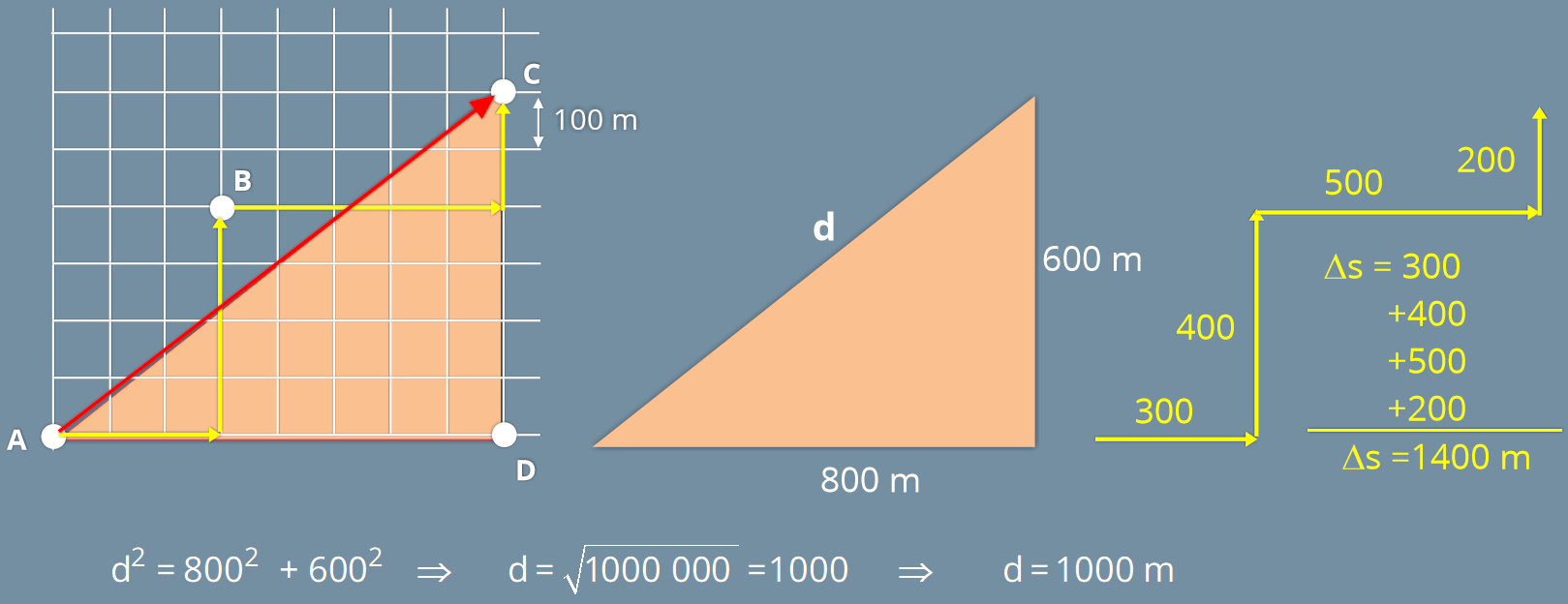
Resposta: A
Para verificar quais itens são verdadeiros, teremos que resolver cada um deles. A figura abaixo nos mostra como é determinado o módulo do vetor deslocamento e a distância percorrida de A até B. Lembre-se quue o vetor deslocamento tem início em A e termina em B.
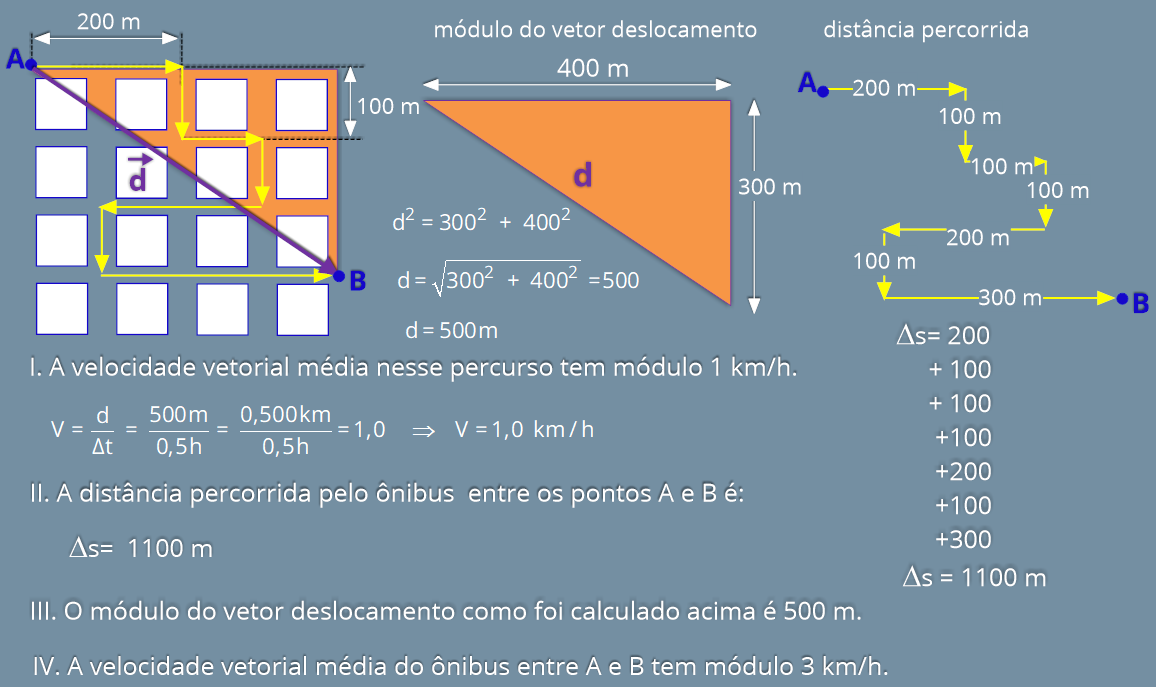Verificamos que as afirmações I e III são as corretas.
Verificamos que as afirmações I e III são as corretas.
Resposta: E
Para determinar a velocidade média vetorial, é necessário deteminar o módulo do vetor deslocamento (d). Seguindo a orientação do texto do exercício, a orientação nordeste -vetor a - é perpendicular com o sudeste - vetor b- formando um triângulo retângulo como mostra a figura abaixo. Neste caso o vetor deslocamento (d), será a hipotenusa do triângulo. Por pitágoras determinamos o valor de d.
Resposta: D
Para determinar a velocidade média vetorial, é necessário deteminar o módulo do vetor deslocamento (d), que tem início em M até a posição final Q, como é mostrado na figura abaixo. Para determinar a deslocamento (d) devemos procurar um outro triângulo retângulo, onde a hipotenusa é d. Por pitágoras determinamos o valor de d. O tempo vai de t = 0s até t = 2,0 s.
Resposta: B
Para determinar a velocidade média escalar, é necessário deteminar o espaço percorrido, que tem início em M, passa por N, depois P, e finalmente Q, como é mostrado na figura abaixo. Para determinar a distância de N até P, é necessário construir um triângulo retângulo para determinar o valor da hipotenusa (lado a). Em seguida somamos as distâncias do ponto M até Q. O tempo está indicado na figura, que inicia em t = 0 s até t = 2,0 s.
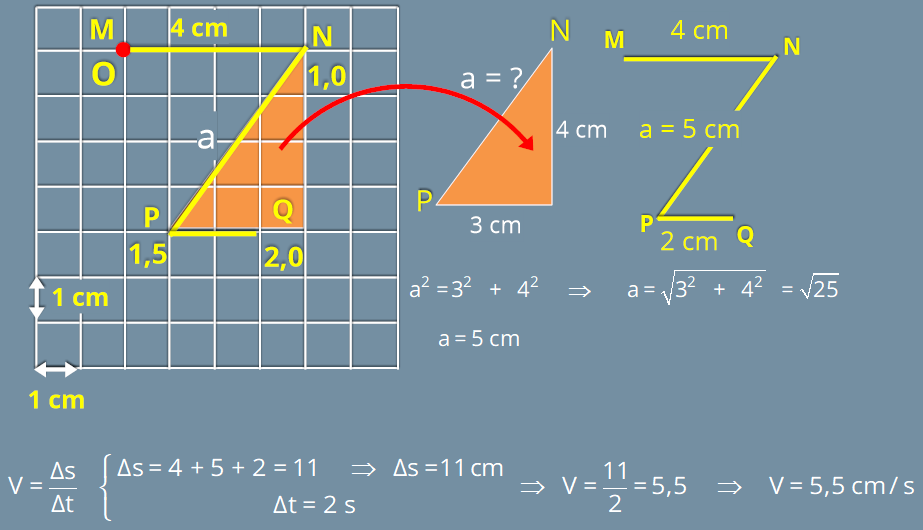
Resposta: B
O Vetor deslocamento, pode ser obtido na figura fornecida pelo exercício, ele inicia na posição A e termina na posição final B, como mostra a Figura.
Perceba que através de um triângulo retângulo é possivel determinar o módulo do vetor deslocamento. Nestes casos o vetor deslocamento acaba sendo a hipotenusa de um triângulo retângulo.
Como cada um dos lados do triângulo valem 3 m e 6 m. Por pitágoras determinamos o módulo do vetor deslocamento
Resposta: B
Sabendo que em um movimento curvelíneo o vetor velocidade é tangente a curva, a única situação apresentada na figura é o de número II.
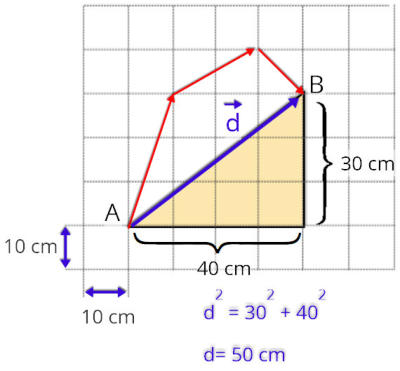
O Vetor deslocamento, pode ser obtido na figura fornecida pelo exercício, ele inicia na posição A e termina na posição final B, como mostra a figura abaixo.
Perceba que através do quadriculado é possivel determinar o módulo do vetor deslocamento. Nestes casos o vetor deslocamento acaba sendo a hipotenusa de um triângulo retângulo.
Como cada quadrado vale 10 um, assim os lados do triângulo valem 40 um e 30 um.
Por pitágoras determinamos o módulo do vetor deslocamento, em seguida determinamos o móduloda velocidade vetorial.
Resposta: D
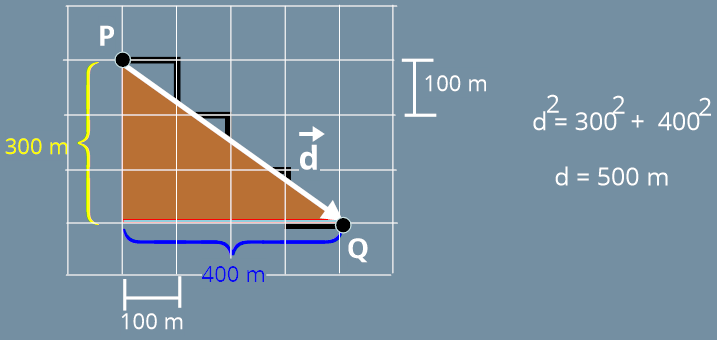
O Vetor deslocamento, pode ser obtido na figura fornecida pelo exercício, ele inicia na posição P e termina na posição final Q, como mostra a Figura abaixo.
Perceba que através do quadriculado é possivel determinar o módulo do vetor deslocamento. Nestes casos o vetor deslocamento acaba sendo a hipotenusa de um triângulo retângulo.
Como cada quadrado vale 100 m, assim os lados do triângulo valem 400 m e 300 m. Por pitágoras determinamos o módulo do vetor deslocamento
