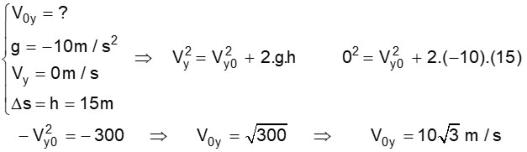© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física

Cinemática

Capítulo 3.6 – Lançamento oblíquo - balística
3.6.a Lançamento oblíquo
Quando
lançamos
um
projétil
para
o
alto,
formando
um
ângulo
em
relação
à
horizontal,
estamos
diante
de
um
lançamento
oblíquo
.
Esse
tipo
de
movimento
faz
parte
da
categoria
dos
movimentos
de
projéteis,
nos
quais
a
única
força
que
atua
sobre
o
corpo,
após
o
lançamento,
é
a
força da gravidade.
Essa
característica
o
aproxima
do
lançamento
horizontal,
já
que,
em
ambos
os
casos,
a
aceleração
gravitacional
atua
apenas
no
sentido
vertical.
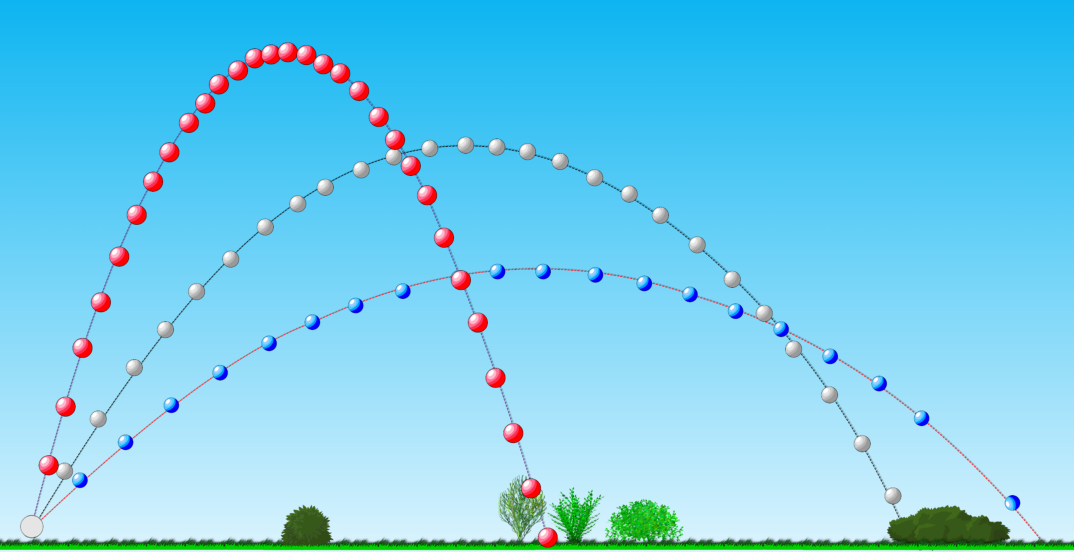
Observando
as
trajetórias
dos
três
projéteis
representadas
na
figura
a
seguir,
notamos
que
todas
descrevem
arcos
de
parábolas,
o
que
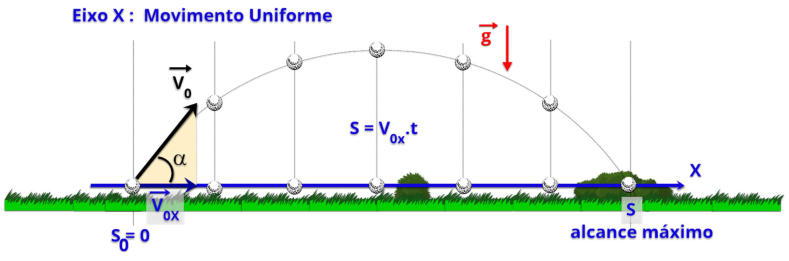
reforça a ideia de que o lançamento oblíquo compartilha importantes semelhanças com o lançamento horizontal.
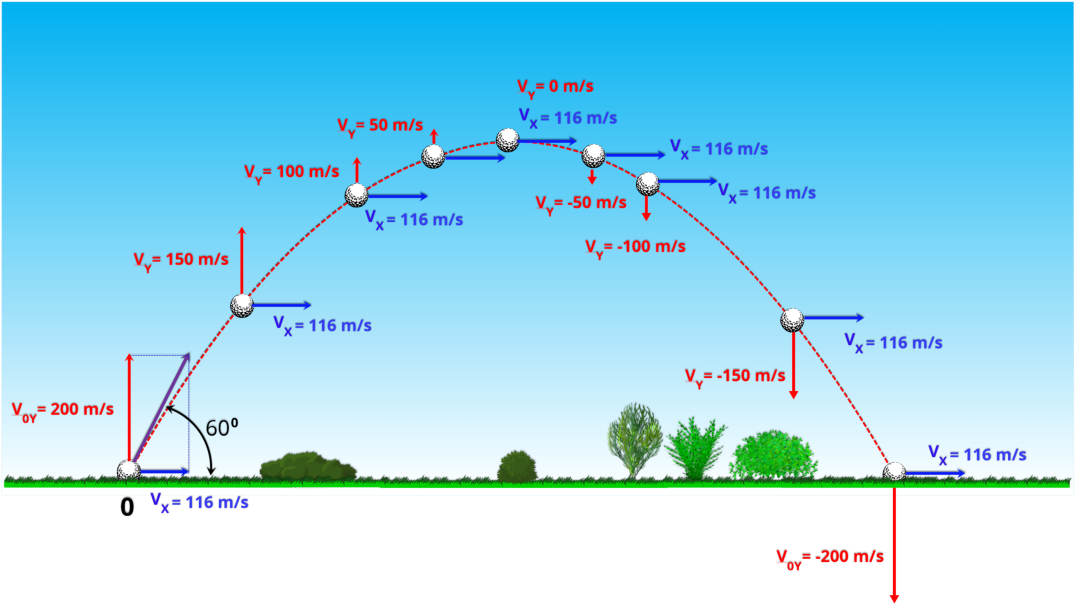
Considerando
um
projétil
lançado
com
um
ângulo
de
60°
em
relação
à
horizontal,
vamos
representar,
por
meio
de
um
diagrama,
as
componentes da velocidade nos eixos x (horizontal) e y (vertical).
Nesse exemplo, o objeto é lançado com uma
velocidade inicial de 233 m/s.
Essa velocidade pode ser decomposta em duas componentes:
•
Componente vertical (eixo y):
200 m/s para cima.
•
C
omponente horizontal (eixo x):
aproximadamente 116 m/s para a direita.
O objetivo do diagrama é ilustrar um conceito fundamental do movimento de projéteis:
A
componente
horizontal
da
velocidade
permanece
constante
durante
toda
a
trajetória,
enquanto
a
componente
vertical
sofre
variações regulares, devido à aceleração da gravidade.
Considerando
a
gravidade
como
g
=
10
m/s²
,
a
velocidade
vertical
é
alterada
em
10
m/s
a
cada
segundo
—
diminuindo
na
subida,
até
atingir zero no ponto mais alto, e aumentando novamente (no sentido oposto) durante a descida.
Este
diagrama
evidencia
a
independência
entre
os
movimentos
horizontal
e
vertical.
A
aceleração
vertical
não
afeta
a
velocidade
horizontal, o que é essencial para compreender a forma parabólica da trajetória do projétil.
No
vídeo
abaixo,
são
feitos
vários
lançamentos
com
diferentes
ângulos,
note
que
em
todos
eles
a
trajetória
é
um
arco
de
parábola,
perceba
o
que
ocorre
com
a
altura
máxima
e
o
alcance
máximo.
Esse
tipo
de
movimento
pode
ser
estudado
pela
decomposição
de
dois
movimentos,
no
eixo
x
é
o
MRU
e
no
eixo
y
o
MRUV.
Na
sequência
de
lançamentos,
notamos
duas
situações
importantes;
quando
o
ângulo
de
lançamento é 45º, o projétil atinge o alcance máximo, a altura máxima ocorre com ângulo de 90º.
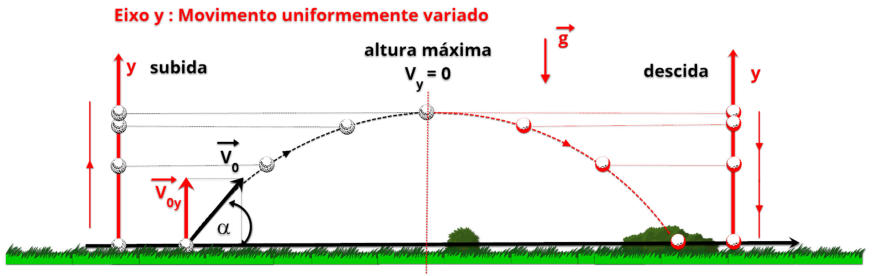
Ao projetarmos o
deslocamento da bola no eixo y,
observamos duas fases distintas do movimento:
1
.
A
subida,
até atingir a altura máxima;
2
.
A
descida,
a partir desse ponto até o solo.
Ambas
as
fases
correspondem
a
um
movimento
retilíneo
uniformemente
variado
(MRUV),
já
que
há
uma
aceleração
constante
—
a
aceleração da gravidade
, que atua sempre no sentido vertical e para baixo.
Para
analisar
esse
movimento,
é
necessário
decompor
a
velocidade
inicial
no
eixo
y.
Essa
componente
vertical
da
velocidade
diminui
gradualmente
durante
a
subida,
devido
à
ação
da
gravidade,
até
se
tornar
nula
no
ponto
mais
alto
da
trajetória
.
Esse
é
o
instante
em
que
o
projétil atinge sua altura máxima.
A
partir
daí,
inicia-se
a
fase
de
descida,
na
qual
a
velocidade
vertical
aumenta
novamente,
agora
no
sentido
oposto
(para
baixo),
também
de forma uniformemente acelerada.
Vamos,
inicialmente,
analisar
o
que
ocorre
com
a
projeção
do
movimento
da
bola
no
eixo
x,
à
medida
que
ela
descreve
um
arco
parabólico.
Ao
observarmos
essa
projeção,
notamos
que
as
distâncias
percorridas
em
intervalos
de
tempo
iguais
são
também
iguais,
o
que
caracteriza
um
movimento
retilíneo
uniforme
(MRU)
.
Isso
significa
que,
ao
longo
do
eixo
horizontal,
não
há
aceleração
—
a
velocidade
permanece constante.
Quando
decompomos
a
velocidade
do
projétil
no
eixo
x,
obtemos
sua
componente
horizontal,
que
se
mantém
constante
durante
toda
a
trajetória.
Isso
ocorre
porque
nenhuma
força
atua
na
direção
horizontal
(desconsiderando
a
resistência
do
ar),
o
que
garante
que
o
movimento
no eixo x seja uniforme.
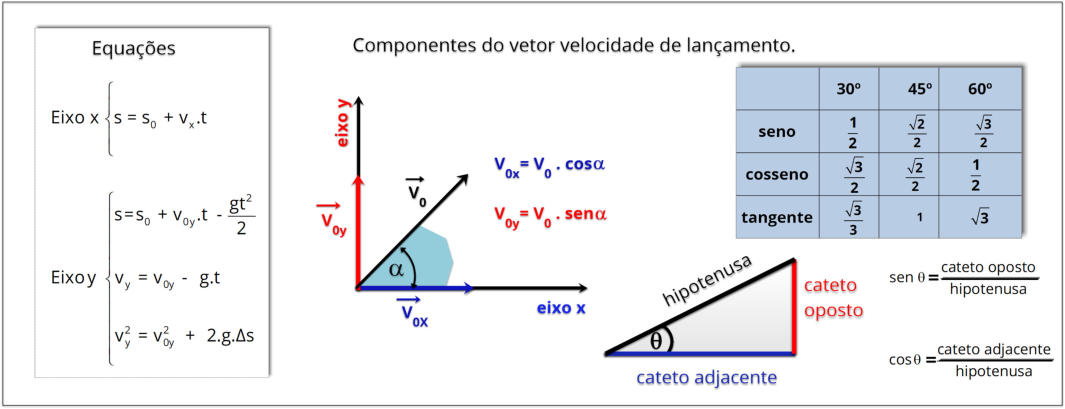
Na decomposição de vetores é bom lembrar das propriedades do triângulo retângulo
Quem
realmente
vai
dar
a
descrição
exata
do
movimento
balístico
é
Galileo
Galilei,
ao
mostrar
que
aquela
curva
era
uma
parábola,
mais
tarde
Isaac
Newton
na
sua
lei
da
gravitação
universal
explicou
o
motivo desta trajetória ser curvilínea.
R1.
Um
projétil,
lançado
no
ponto,
descreve
uma
trajetória
parabólica.
O
movimento
ocorre
no
campo
gravitacional
terrestre,
e
a
força
da
resistência
do
ar
é
desprezível.
O
lançamento
do
projétil
ocorre
com
uma
velocidade
inicial
V
0
=
100
m/s,
numa
direção
que
forma
um
ângulo
de 30º. Adotando g = 10 m/s
2
e cos 30º = 0,5 e sen 30º= 0,87, determine:
a) os módulos das componentes horizontal e vertical da velocidade inicial;
b) o instante em que o corpo atinge o ponto mais alto da trajetória.
Resolução:
R2.
(FEI-SP) Um projétil é lançado do solo numa direção que forma o ângulo a com a horizontal. Sabe-se que ele atinge uma altura máxima
h
máx
=
15
m
e
que
sua
velocidade
no
ponto
de
altura
máxima
é
V
=
10
m/s.
Determine
a
sua
velocidade
inicial
e
o
ângulo
a
de
lançamento.
Adote g = 10 m/s
2
.
3.6.c
Exercícios propostos
P1.
Um
corpo
é
lançado
obliquamente
no
vácuo
com
velocidade
inicial
V
0
=
360
km/h,
que
forma
com
a
horizontal
um
ângulo
de
30°,
tal
que
sen 30° = 0,50 e
cos 30° = 0,87. Adotando g = 10 m/s² .
Determine :
a) os módulos das velocidades horizontal e vertical no início do movimento
b) o instante em que o corpo atinge o ponto mais alto da trajetória
c) altura máxima
d) o alcance do movimento
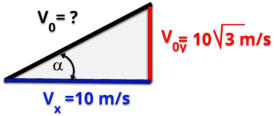
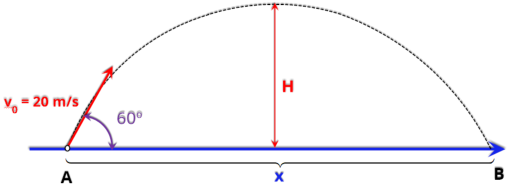
P2.
(UNIFEI)
Uma
pedra
é
lançada
para
cima
fazendo
um
ângulo
de
60°
com
a
horizontal,
e
uma
velocidade
inicial
de
20
m/s,
conforme
a
figura
ao lado. (Adotar
g = 10 m/s
2
)
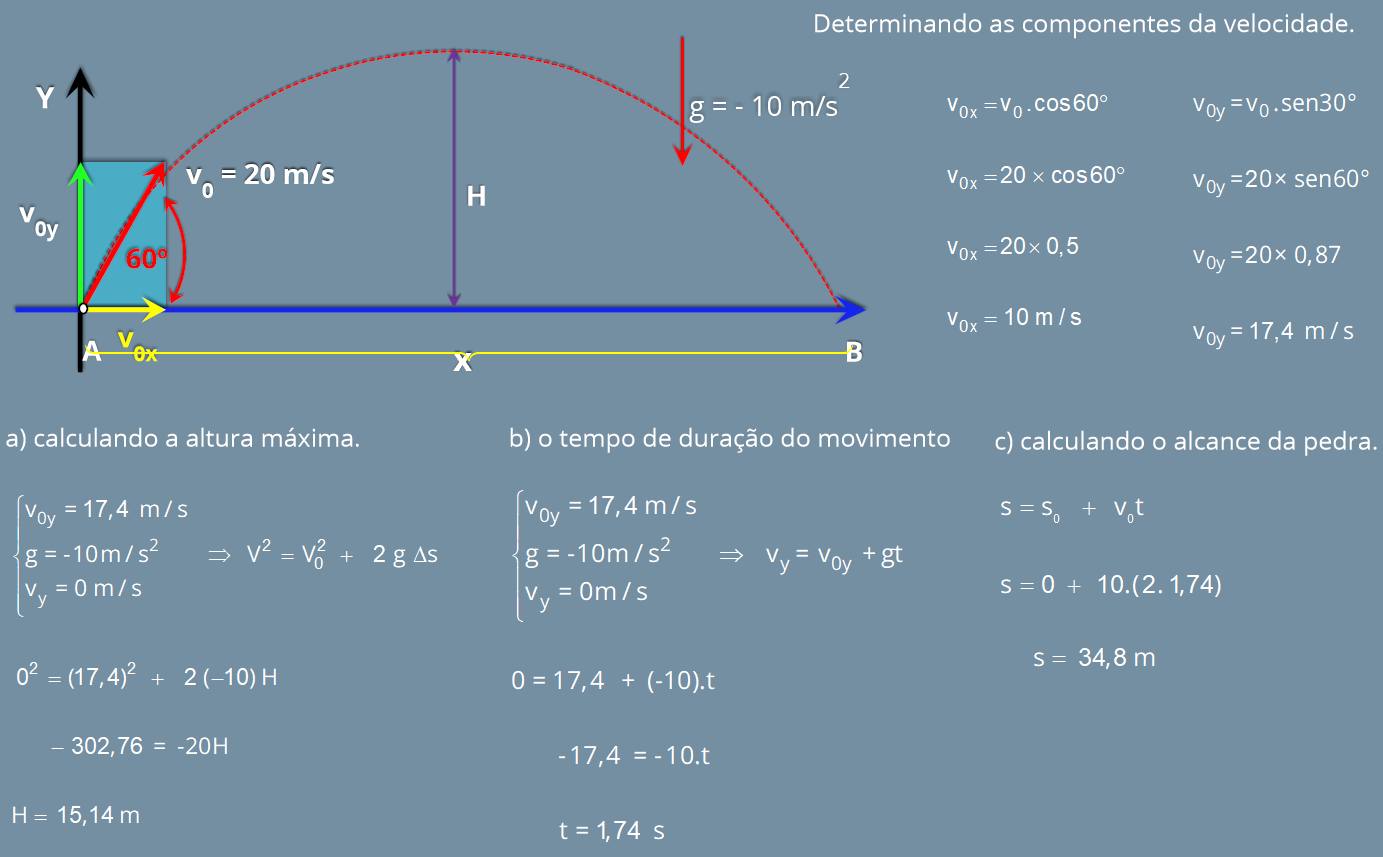
a) Qual a altura máxima atingida pelo objeto?
b) Qual o tempo total do movimento?
c) Qual o valor de x?
P3.
(STA
CASA-SP)
Um
canhão,
em
solo
plano
e
horizontal,
dispara
uma
bala,
com
ângulo
de
tiro
de
30°
.
A
velocidade
inicial
da
bala
é
500
m/s.
Sendo g = 10 m/s
2
o valor da aceleração da gravidade no local, qual a altura máxima da bala em relação ao solo, em km?
P4.
(PUCC-SP)
Calcular
o
alcance
de
um
projétil
lançado
por
um
morteiro
com
velocidade
inicial
de
100
m/s,
sabendo-se
que
o
ângulo
formado
entre o morteiro e a horizontal é de 30°. Adotar g = 10 m/s
2
.
P5.
(OSEC-SP)
Um
corpo
é
lançado
obliquamente
para
cima,
formando
um
ângulo
de
30
0
com
a
horizontal.
Sabe-se
que
ele
atinge
uma
altura
máxima h
máx
= 15 m e que sua velocidade no ponto de altura máxima é v = 10 m/s. Determine a sua velocidade inicial. Adotar g = 10 m/s
2
.
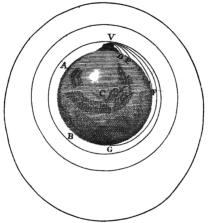
No
diagrama
publicado
por
Newton,
ele
mostra
pela
ilustração
que
ao
lançar
projéteis
com
velocidades
diferentes,
é
possível
atingir
um
valor
determinado,
que
colocaria
o
corpo
em
órbita.
Desta
maneira
ele
tentava
mostrar
a
importância
da
atração
exercida
pela
Terra
sobre
um
projétil.
Na
figura,
são
representadas
as
curvas
que
um
corpo
descreveria
se
fosse
atirado
na
direção
horizontal
de
cima
de
uma
alta
montanha
a
velocidades
cada vez maiores. Ilustração utilizado por Newton, em seu livro “De Um Tratado sobre o sistema do mundo” (1728)
3.6.b
Exercícios resolvidos
Por conta do grande número de dados fornecidos no enunciado da questão, precisamos ser organizados. Vamos ser objetivos e
práticos na resolução dos exercícios. A seguir, estão algumas etapas importantes que facilitam muito a análise e a solução de problemas
envolvendo lançamento oblíquo:
MRU no eixo x (horizontal, sem aceleração)
MRUV no eixo y (vertical, com aceleração da gravidade)
Aqui estão as etapas principais para resolver um exerccio sobre lançamento oblíquo:
1. Identificar os dados do problema
Anote todas as informações fornecidas no enunciado:
Velocidade inicial V
0
Ângulo de lançamento (θ)
Altura inicial (se houver)
Posição final (se for pedida)
Tempo (se dado ou a ser calculado)
Aceleração da gravidade (geralmente g = 9,8 m/s² ou 10 m/s²)
2. Desenhe um esquema da situação descrita. Representar o cenário graficamente ajuda a visualizar a trajetória, identificar os vetores.
3. Decompor a velocidade inicial
Use trigonometria para encontrar as componentes da velocidade:
V
0X
= V
0
·cos(θ) componente horizontal
V
0Y
= V
0
· sen(θ) componente vertical
4. Escolha as equações adequadas para cada eixo:
5. Decida por onde começar: em muitos casos, é mais fácil encontrar o tempo usando os dados do eixo Y (altura, por exemplo), e só depois
aplicá-lo no eixo X para calcular o alcance ou a posição horizontal.
Essas etapas são fundamentais para resolver corretamente os problemas. A clareza na separação dos dados e o uso estratégico do
tempo tornam a análise mais simples e precisa.










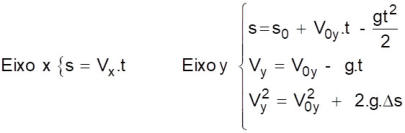
2. Desenhe um esquema da situação descrita.
1. Identificar os dados do problema. Anote todas
as informações fornecidas no enunciado:
Velocidade inicial: V
0
= 100 m/s,
Ângulo de lançamento: θ = 30º,
Aceleração da gravidade: g = -10 m/s².



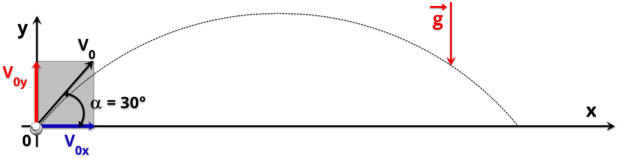
3. Decompor a velocidade inicial
Use trigonometria para encontrar as componentes
da velocidade:
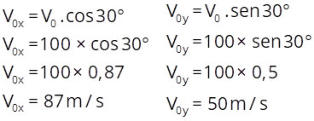
4. Escolha as equações adequadas para cada eixo
5. O tempo (t) é a variável que conecta os dois eixos, pois é o mesmo
para o movimento horizontal e vertical.
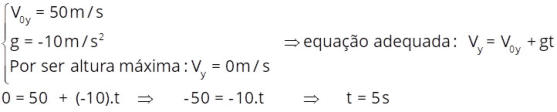
Respostas:
a) os módulos das componentes horizontal e vertical da velocidade inicial;
V
0X
= 87 m/s e V
0Y
= 50 m/s
b) o instante em que o corpo atinge o ponto mais alto da trajetória.
t
= 5 s
2. Desenhe um esquema da situação descrita.
1. Identificar os dados do problema. Anote todas as
informações fornecidas no enunciado:
velocidade no ponto de altura máxima V
Y
= 10 m/s,
Ângulo de lançamento: a = ?,
Aceleração da gravidade: g = -10 m/s².
Altura máxima: h
máx
= 15 m.




4. Escolha as equações adequadas para cada eixo
Neste caso os dados são na maioria no eixo y, inclusive foi
fornecida a altura máxima, sem termos o valor do tempo,
isso justifica usar Torricelli.
Respostas:
V
0
= 20 m/s e o ângulo a = 60º
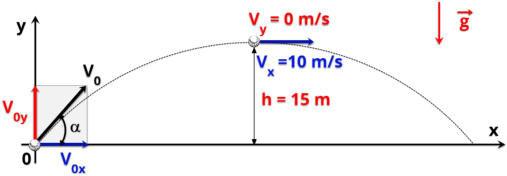
Neste, caso mudaremos a sequência das resoluções propostas, iremos para a etapa 4 e posteriormente a etapa 3.
3. Decompor a velocidade inicial - Use trigonometria para
encontrar as componentes da velocidade: