



© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física

Cinemática

3.4 Transmissão do movimento Circular II
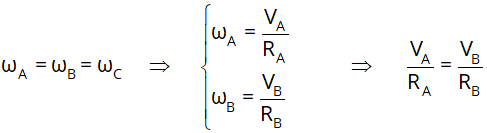
3.4.a Polias e engrenagens em um mesmo eixo.
R4.
(UFPE
2010)
Uma
bicicleta
possui
duas
catracas,
uma
de
raio
6,0
cm,
e
outra
de
raio
4,5
cm.
Um
ciclista
move-se
com
velocidade
uniforme
de
12
km/h
usando
a
catraca
de
6,0
cm.
Com
o
objetivo
de
aumentar
a
sua
velocidade,
o
ciclista
muda
para
a
catraca
de
4,5
cm
mantendo
a
mesma velocidade angular dos pedais. Determine a velocidade final da bicicleta, em km/h.
a) 2 m/s b) 4 m/s c) 8 m/s d) 12 m/s e) 16 m/
3.4.c
Exercícios resolvidos
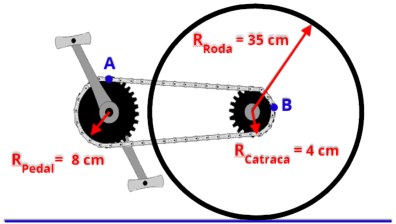
R5.
(UFPR
2017)
O
raio
da
roda
de
uma
bicicleta
é
35
cm.
No
centro
da
roda
tem
uma
engrenagem
cujo
raio
é
4
cm.
Esta
engrenagem,
por
meio
de
uma
corrente,
é
acionada
por
outra
engrenagem
com
raio
8
cm.
O
pedal
da
bicicleta
movimenta
a
engrenagem
de
raio
8
cm.
Um
ciclista
desloca-se,
fazendo
uso
desta
bicicleta
e,
a
cada
três
voltas
do
pedal,
é
necessário
o
transcurso
de
2
s.
Determine:
Obs.:
represente
a
constante
pi
apenas
por
p.
Não
é
necessário
substituir
o
seu
valor
numérico
nos
cálculos.
a) A velocidade angular da engrenagem do pedal, em radianos por segundo.
b)
O
valor
absoluto
da
velocidade
linear
de
um
dos
elos
da
corrente
que
liga
a
engrenagem
do
pedal à engrenagem da roda.
c)
A
distância
percorrida
pela
bicicleta
se
o
ciclista
mantiver
a
velocidade
constante,
nas
condições
citadas no enunciado do problema, durante 5 minutos?
Resolução:
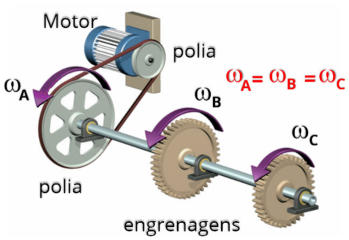
As
associações
de
engrenagens,
também
conhecidas
como
“trem
de
engrenagem”
é
um
conjunto
destinado
a
transmitir
rotações,
é
compostos
por
duas
ou
mais
engrenagens
semelhantes
à
figura
abaixo.
Nessas
situações,
provavelmente
também
teremos
engrenagens
conectadas
por
meio
de
um
eixo,
como
as
engrenagens
B
e
C.
Em
tais
situações,
as
engrenagens
no
mesmo
eixo
terão
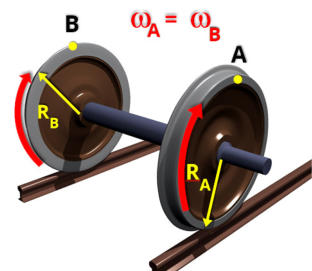
deslocamentos angulares e velocidades angulares iguais.
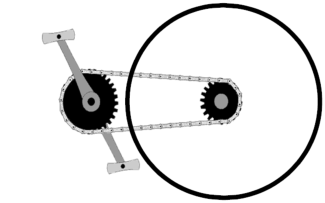
O
diagrama
ao
lado
mostra
duas
polias
associadas
por
uma
cinta,
onde
uma
das polias e as engrenagens B e C estão no mesmo eixo.
É
facil
entender
que
quando
o
eixo
dá
uma
volta,
todas
as
rodas
também
dão
uma volta, mesmo possuindo raios diferentes, assim podemos escrever:
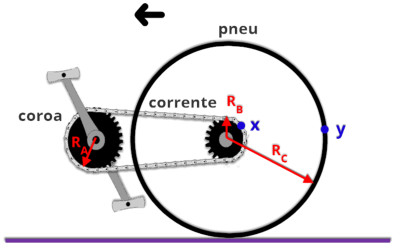
R6.
(Ufu
2018)
Assuma
que
as
dimensões
das
engrenagens
e
do
pneu
de
uma
bicicleta
sejam as indicadas na figura ao lado.
Dados R
A
= 18 cm; R
B
= 6 cm; R
C
= 20 cm (figura fora de escala)
a)
Considerando-se
os
pontos
x
e
y
indicados
na
figura,
qual
deles
terá
menor
velocidade linear? Explique sua resposta.
b)
Pedalando
em
uma
bicicleta
com
as
dimensões
descritas,
um
ciclista
foi
instruído
de
que,
para
vencer
uma
corrida,
deve
se
manter
à
velocidade
constante
de
65
km/h
durante
toda
a
prova.
Qual
o
número
de
pedaladas
por
segundo
que
ele
deve
dar
para
manter a velocidade indicada?
Resolução:
a
)
Sabemos
que
a
catraca
e
a
roda
traseira
estão
ligadas
no
mesmo
eixo
de
rotação,
desta
forma
os
pontos
X
e
Y
possuem
a
mesma
velocidade
angular. Sendo assim:
Portanto, o ponto Y terá maior velocidade linear.

b) Vamos determinar o número de pedaladas necessárias para manter a velocidade de 65 km/h, ou seja 18 m/s.
significa que o ciclista deverá dar aproximadamente 5,4 pedaladas por segundo

a
)
Como
está
indicado
na
figura
ao
lado,
os
raios
nas
suas
respectivas
rodas.
Para
determinar
a
velocidade
angular,
vamos
inicialmente
determinar
a
frequência
do
movimento.
b)
os
elos
da
corrente
possuem
a
mesma
velocidade
que
as
extremidades
da
catraca
e do pedal. Na figura representamos por A e B. Portanto:
V
A
= V
B
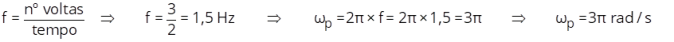
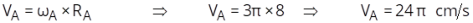
c)
Para
determinar
a
distância
percorrida
pelo
ciclista
devemos
considerar
a
roda
da
bicicleta,
por
ser
a
que
permite
o
deslocamento.
Para
sabet
a distânci, precisamos determinar a velocidade da roda, ´ja que o tempo foi dado, t = 5 min = 300 s.
V
Roda
= 2.p.f
Roda.
R
Roda
Vamos determinar a frequência da Roda. Como a roda e a catraca possuem a mesma velocidade angular, podemos afirmar que suas
frequencias são iguais.

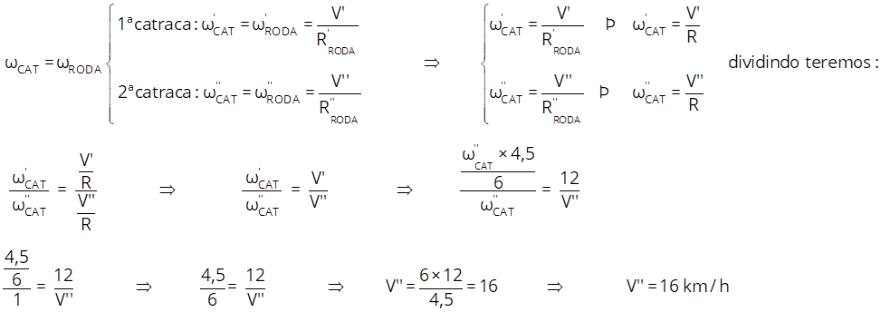
Resolução:
Como a coroa e catraca estão ligadas pela corrente, suas velocidades lineares são iguais.
Como a velocidade angular da roda da bicicleta é igual à velocidade angular da catraca.
Dados:
Raio da roda da bicicleta: R
RODA
Raio inicial da catraca: = 6 cm
Raio final da catraca: = 4,5 cm
Raio da coroa: R
COROA
Velocidade inicial da bicicleta: = 12 km/h
Velocidade final da bicicleta: = ?

R3.
A
engrenagem
principal
é
acionada
por
um
motor
que
gira
com
uma
velocidade
angular
de
60
rad/s.
Conhecendo
o
número
de
dentes
de
cada
engrenagem,
indicado
na figura ao lado, determine a velocidade angular da última engrenagem de 8 dentes.
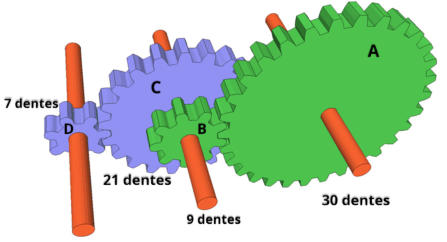
R2.
Considerando
a
roda
verde
é
ligada
a
um
motor
com
velocidade
angular
30
rad/s.
Determine
no
processo
de
transmissão
de
movimento,
qual
deve
ser
a
velocidade
angular da engrenagem D.
Resolução:
A
frequência
de
rotação
de
uma
engrenagem,
depende
do
raio
ou
do
número
de
dentes.
Se
a
engrenagem
A
possui
30
dentes
e
a
B
9
dentes,
podemos
estabelecer
uma
relação
entre
a
engrenagem
B
e
A
(cor
verde).
Se
a
velocidade
angular
de
A
é
30
rad/s,
a
de
B
pode
ser
determinada,
considerando
que
as
duas
engrenagens
giram
em
contato,
neste caso a velocidade linear nos extremos das duas engrenagem é a mesma, assim:
A
engrenagem
inicial
possui
uma
velocidade
angular
de
30
rad/s,
a
última
engrenagem
é
de
300
rad/s.
Concluimos
que
a
associação
de
engrenagens
aumentou a rotação em 10 vezes.

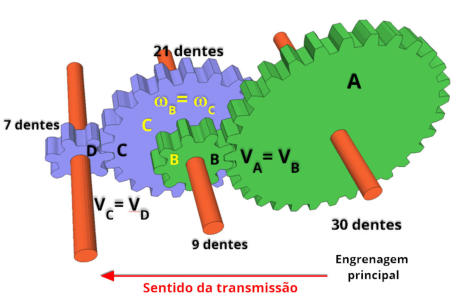
Imagem gentilmente cedida por Mathias Wandel
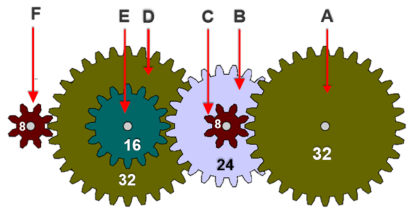
Resolução:
A
frequência
de
rotação
de
uma
engrenagem,
depende
do
raio
ou
do
número
de
dentes.
Na
figura
ao
lado
vemos
que
a
engrenagem
A,
será
acionada
por
um
motor
e
ocorrerá
a
transmissão
de
movimento
de
A
até
F.
Em
cada
engrenagem
vemos
o
número
de
dentes,
possibilitando
determinar
a
velocidade
angular
da
última
engrenagem
F.
Para
facilitar
a
compreensão
vamos
dividir
a
figura
em
cada
etapa
da
transmissão do movimento.
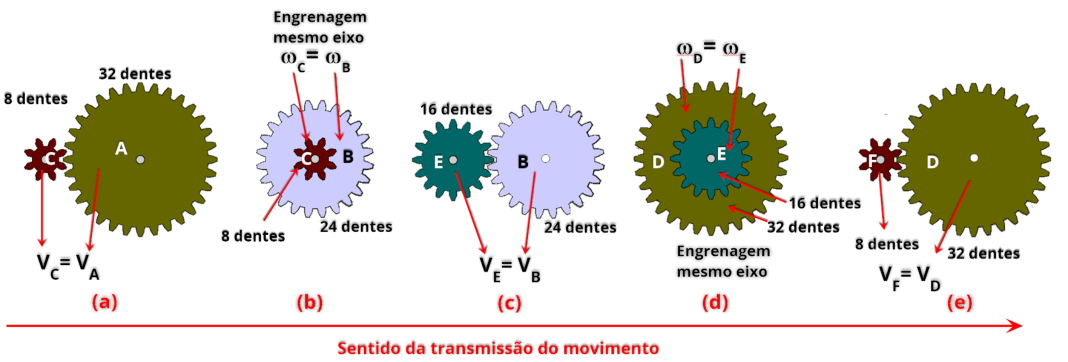
Em (a) teremos:
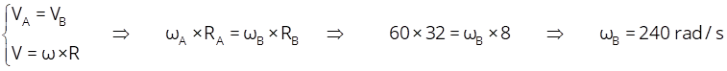
Em (b) teremos:

E
m (c) teremos:
Em (d) teremos:



Em (e) teremos:
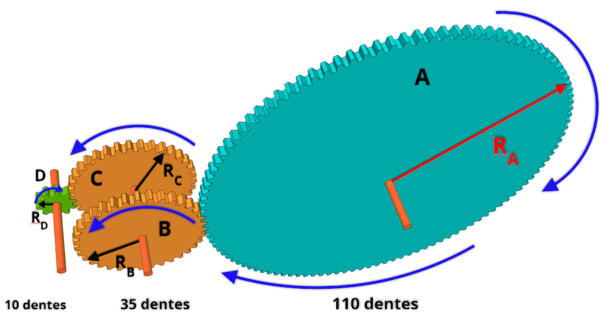
R1.
Considere
as
quatro
engrenagens
acopladas
simbolizadas
na
figura
ao
lado.
A
engrenagem
A
tem
110
dentes
e
gira
no
sentido
horário,
indicado
na
figura,
com
velocidade
angular
de
120
rpm
(rotação
por
minuto).
A
engrenagem
B
e
C
possuem
35 dentes e a D 10 dentes.
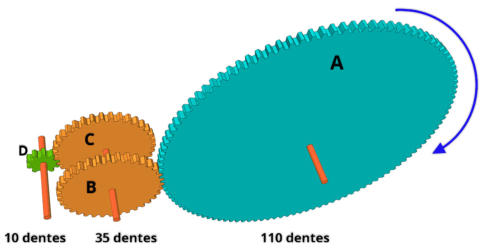
a) Qual é o sentido de rotação da engrenagem D?
b) Quanto vale a velocidade tangencial da engrenagem A em dentes/min?
c) Qual é a frequência de rotação (em rpm) da engrenagem D?
Resolução:
a)
Analizando
a
figura,
começando
pela
engrenagem
A,
cujo
sentido
é
o
horário,
pode-se determinar o sentido de cada uma delas até chegar na engrenagem D.
b)
Vamos
determinar
a
velocidade
linear
da
engrenagem
A.
A
frequência
f
A
=
120
rpm,
siginifica
que
ela
gira
120
vezes
em
um
único
minuto,
sendo
que
cada
volta
passam
110
dentes.
Para
determinar a velocidade em dentes por minuto teremos:
V = 120 voltas x 110 dentes= 13 200
V = 13 200 dentes por minuto
-
Quando
duas
engrenagens
ou
polias
estão
em
contato,
o
sentido
do
movimento são opostos, Se A é horário, o de B será anti-horário.
-
Quando
duas
polias
ou
engrenagens
possuem
o
mesmo
eixo
de
rotação
(B
e
C)
o
sentido
de
rotação
das
duas
será
o
mesmo.
B
e
C
possuem um movimento anti-horário.
Concluimos
que
C
e
D
estão
em
contato,
logo
giram
em
sentidos
opostos,
D será no sentido horário.
c)
Engrenagem A e B, como estão em contato, vale: V
A
=V
B
As engrenagens C e D estão em contato, logo: V
D
=V
C
Imagem gentilmente cedida por Mathias Wandel
Engrenagem
Principal
3.4.d
Testes propostos
T6.
(Albert
Einstein
-
Medicina
2024)
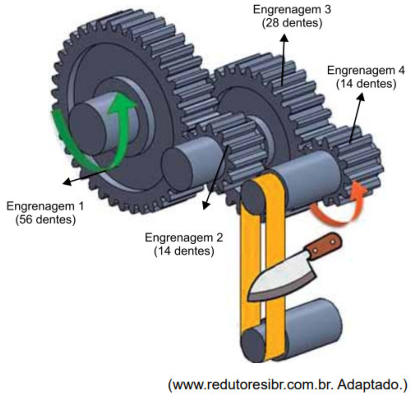
O
mecanismo
mostrado
na
figura
foi
adaptado
para
afiar
facas.
Ele
é
constituído
de
engrenagens
de
tamanhos
diferentes
e
de
uma
fita
abrasiva.
O
motor
que
faz
a
engrenagem
1
girar
tem
frequência
de
75
rpm
e
os
pinos
com
os
quais
a
fita
abrasiva
faz
contato
têm
raios
de
curvatura
iguais,
medindo
5
cm
cada
um.
Nesse
procedimento,
a
faca
é
mantida
em
contato
com
a
fita
abrasiva
e
em repouso em relação ao solo.
Sabendo
que
o
número
de
dentes
na
periferia
de
uma
engrenagem
é
diretamente
proporcional
ao
raio
dessa
engrenagem,
que
não
há
escorregamento
entre
a
fita
abrasiva
e
os
pinos
com
os
quais
ela
faz
contato
e
adotando
π=3,
a
velocidade
escalar
com que a fita passa pela faca que está sendo afiada é de
a) 2,0 m/s. b) 2,5 m/s. c) 3,5 m/s. d) 3,0 m/s. e) 1,5 m/s.
T5.
(Enem
2016)
A
invenção
e
o
acoplamento
entre
engrenagens
revolucionaram
a
ciência
na
época
e
propiciaram
a
invenção
de
várias
tecnologias,
como
os
relógios.
Ao
construir
um
pequeno
cronômetro,
um
relojoeiro
usa
o
sistema
de
engrenagens
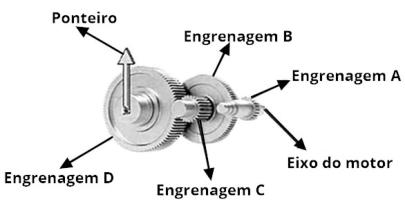
mostrado.
De
acordo
com
a
figura,
um
motor
é
ligado
ao
eixo
e
movimenta
as
engrenagens
fazendo
o
ponteiro
girar.
A
frequência
do
motor
é
de
18
rpm
e
o
número
de dentes das engrenagens está apresentado no quadro.
A frequência de giro do ponteiro, em rpm é
a) 1 b) 2 c) 4 d) 81 e) 162
Engrenagem
Dentes
A
24
B
72
C
36
D
108
T8.
(PUCCamp
2005)
Em
uma
bicicleta
o
ciclista
pedala
na
coroa
e
o
movimento
é
transmitido
à
catraca
pela
corrente.
A
frequência
de
giro
da
catraca
é
igual
à
da
roda.
Supondo
os
diâmetros
da
coroa,
catraca
e
roda
iguais,
respectivamente,
a
15
cm,
5,0
cm
e
60
cm,
a
velocidade
dessa
bicicleta,
em
m/s,
quando
o
ciclista
gira
a
coroa
a
80
rpm, tem módulo mais próximo de
a) 5 b) 7 c) 9 d) 11 e) 14
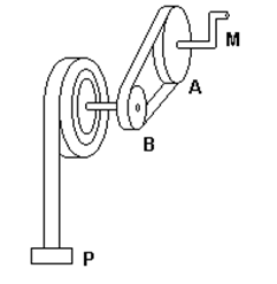
T12.
(Unirio
1999)
O
mecanismo
apresentado
na
figura
anterior
é
utilizado
para
enrolar
mangueiras
após
terem
sido
usadas
no
combate
a
incêndios.
A
mangueira
é
enrolada
sobre
si
mesma,
camada
sobre
camada,
formando
um
carretel
cada
vez
mais
espesso.
Considerando
ser
o
diâmetro
da
polia
A
maior
que
o
diâmetro
da
polia
B,
quando
giramos
a
manivela
M
com
velocidade
constante,
verificamos
que
a
polia
B
gira_______
que
a
polia
A,
enquanto
a
extremidade
P
da
mangueira
sobe
com
o
movimento___________.vcvc
Preenche corretamente as lacunas anteriores a opção:
a) mais rapidamente - acelerado.
b) mais rapidamente - uniforme.
c) com a mesma velocidade - uniforme.
d) mais lentamente - uniforme.
e) mais lentamente - acelerado.
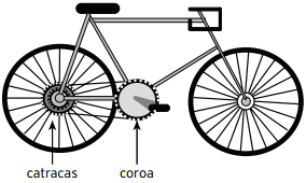
T10.
(Enem
1998)
As
bicicletas
possuem
uma
corrente
que
liga
uma
coroa
dentada
dianteira,
movimentada
pelos
pedais,
a
uma
coroa
localizada
no
eixo
da
roda
traseira,
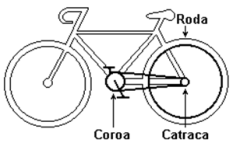
como mostra a figura.
O
número
de
voltas
dadas
pela
roda
traseira
a
cada
pedalada
depende
do
tamanho
relativo destas coroas.
Quando
se
dá
uma
pedalada
na
bicicleta
da
figura
ao
lado
(isto
é,
quando
a
coroa
acionada
pelos
pedais
dá
uma
volta
completa),
qual
é
a
distância
aproximada
percorrida
pela
bicicleta,
sabendo-se
que
o
comprimento
de
um
círculo
de
raio
R
é
igual a 2πR, onde π
≃
3?
a) 1,2 m b) 2,4 m c) 7,2 m d) 14,4 m e) 48,0 m
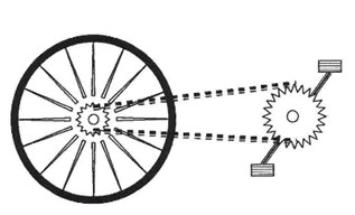
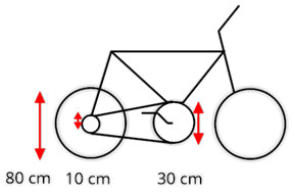
T14.
(UFPR
2012)
Um
ciclista
movimenta-se
com
sua
bicicleta
em
linha
reta
a
uma
velocidade
constante
de
18
km/h.
O
pneu,
devidamente
montado
na
roda,
possui
diâmetro
igual
a
70
cm.
No
centro
da
roda
traseira,
presa
ao
eixo,
há
uma
roda
dentada
de
diâmetro
7,0
cm.
Junto
ao
pedal
e
preso
ao
seu
eixo
há
outra
roda
dentada
de
diâmetro
20
cm.
As
duas
rodas
dentadas
estão
unidas
por
uma
corrente,
conforme
mostra
a
figura.
Não
há
deslizamento
entre
a
corrente
e
as
rodas
dentadas.
Supondo
que
o
ciclista
imprima
aos
pedais
um
movimento
circular
uniforme,
assinale
a
alternativa
correta
para
o
número
de
voltas
por
minuto
que
ele
impõe
aos
pedais
durante esse movimento. Nesta questão, considere .
a) 0,25 rpm. b) 2,50 rpm. c) 5,00 rpm. d) 25,0 rpm. e) 50,0 rpm.
T15.
(UFPB
2012)
Em
uma
bicicleta,
a
transmissão
do
movimento
das
pedaladas
se
faz
através
de
uma
corrente,
acoplando
um
disco
dentado
dianteiro
(coroa)
a
um
disco
dentado
traseiro
(catraca),
sem
que
haja
deslizamento
entre
a
corrente
e
os
discos.
A
catraca,
por
sua
vez,
é
acoplada
à
roda
traseira
de
modo
que
as
velocidades
angulares
da
catraca
e
da
roda
sejam
as
mesmas
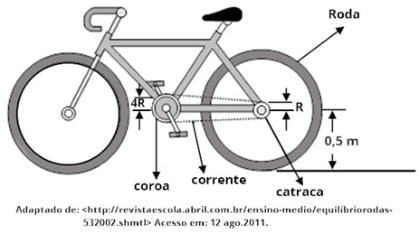
(ver
a
seguir
figura
representativa
de
uma
bicicleta).
Em
uma
corrida
de
bicicleta,
o
ciclista
desloca-se
com
velocidade
escalar
constante,
mantendo
um
ritmo
estável
de
pedaladas,
capaz
de
imprimir
no
disco
dianteiro
uma
velocidade angular de
4
rad/s,
para
uma
configuração
em
que
o
raio
da
coroa
é
4R,
o
raio
da
catraca
é
R
e
o
raio
da
roda
é
0,5
m.
Com
base
no
exposto,
conclui-se
que
a
velocidade
escalar
do
ciclista é:
a) 2 m/s b) 4 m/s c) 8 m/s d) 12 m/s e) 16 m/s
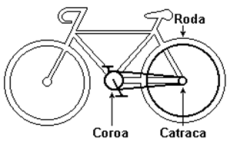
T8.
(PUCCamp
2005)
Em
uma
bicicleta
o
ciclista
pedala
na
coroa
e
o
movimento
é
transmitido
à
catraca
pela
corrente.
A
frequência
de
giro
da
catraca
é
igual
à
da
roda.
Supondo
os
diâmetros
da
coroa,
catraca
e
roda
iguais,
respectivamente,
a
15
cm,
5,0
cm
e
60
cm,
a
velocidade
dessa
bicicleta,
em
m/s,
quando
o
ciclista
gira
a
coroa
a
80
rpm,
tem módulo mais próximo de
a) 5 b) 7 c) 9 d) 11 e) 14
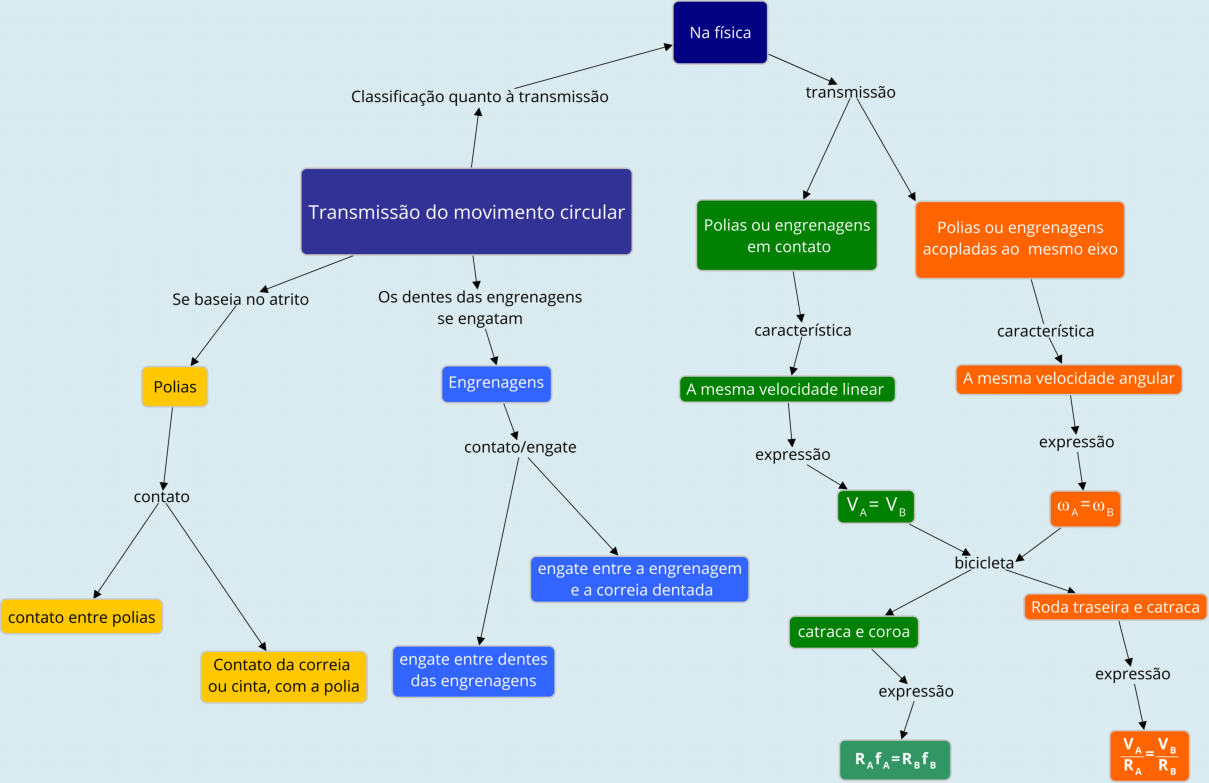
Este
mapa
conceitual
apresenta
uma
visão
geral
dos
exemplos
e
conceitos
vistos
nesta
página,
ele
se
apresenta
na
forma
de
um
conjunto
de
proposições
interconectadas.
O
significado
de
qualquer
conceito
é
a
soma
de
todas
as
ligações
que
contêm
o
conceito.
Para
"ler"
o
mapa
conceitual, comece pelo quadro Transmissão de movimento circular, e vá até os itens mais específicos e os exemplos nas partes mais externas.
3.4.b Mapa conceitual - Revisando a transmissão de movimento

Procure fazer o teu mapa conceitual, vai te ajudar a organizar os conceitos desta lição.



















