


© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física
3.0.c Exercícios propostos
P1.
(UNESP)
No
ensino
médio,
as
grandezas
físicas
costumam
ser
classificadas
em
duas
categorias.
Na
primeira
categoria,
estão
as
grandezas
definidas
apenas
por
um
número
e
uma
unidade
de
medida;
as
grandezas
da
segunda
categoria
requerem,
além
disso,
o
conhecimento
de
sua
direção e de seu sentido.
a) Como são denominadas as duas categorias, na seqüência apresentada?
b) Copie a tabela seguinte em seu caderno de respostas e preencha corretamente as lacunas, indicando uma grandeza física da área de
mecânica e outra da área de eletricidade, para cada uma dessas categorias.
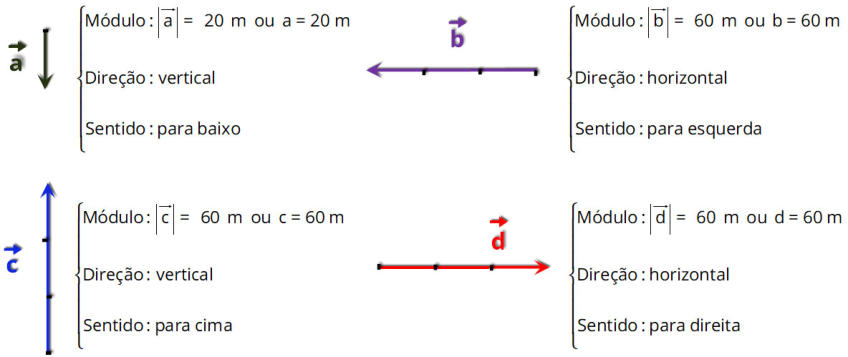
P2.
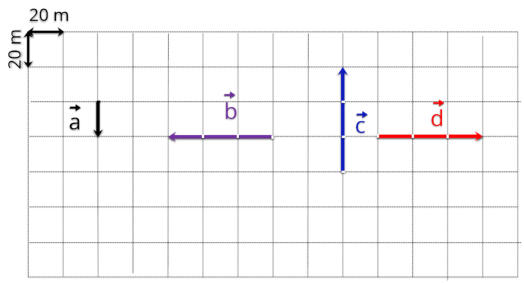
Na figura abaixo estão representados quatro vetores, indique as características destes, o módulo, sentido e direção.
Capítulo 3.0 – Cinemática Vetorial - Vetores
3.0 Introdução as Grandezas vetoriais
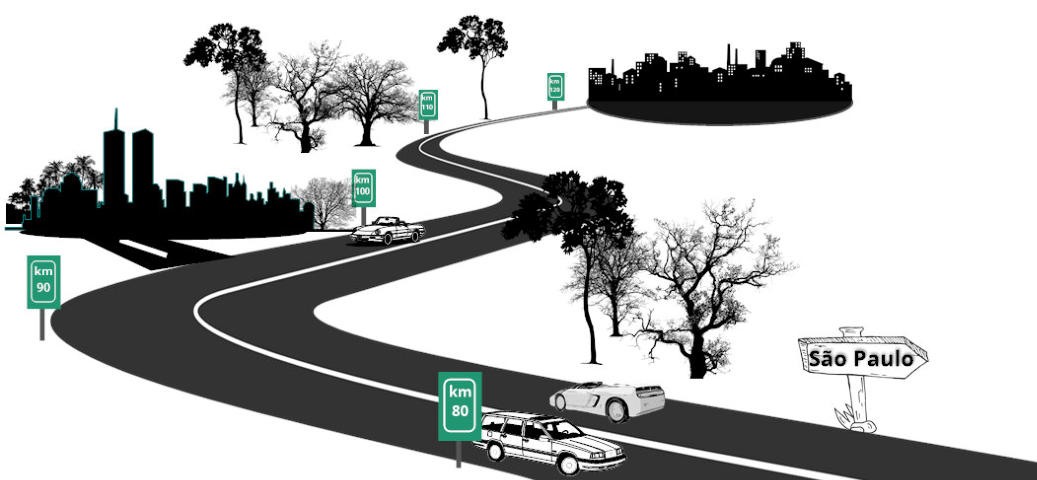
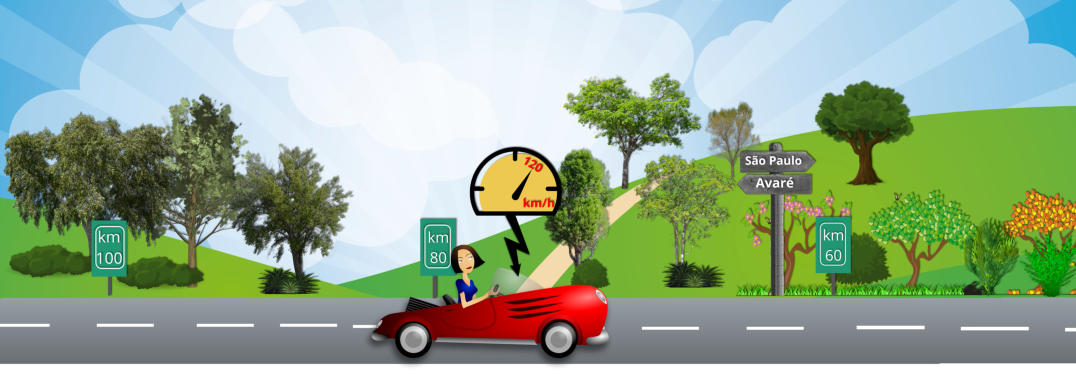
2ª Situação
– “...Estou em um trecho da rodovia, no quilômetro 80, a 120 km/h...”
Nesse
segundo
exemplo,
podemos
imaginar
um
veículo
localizado
no
quilômetro
80
de
uma
rodovia,
com
uma
velocidade
de
120
km/h.
No
entanto,
esses
dois
valores
numéricos,
por
si
só,
não
são
suficientes
para
descrever
completamente
o
movimento
.
Faltam
informações
importantes:
qual é o sentido do deslocamento? O veículo está indo em direção ao interior ou rumo à capital, São Paulo?
Seria
muito
útil
se
tivéssemos
um
esquema
como
o
da
Figura
2
,
que
ilustra
uma
possível
situação
de
movimento
e
ajuda
a
interpretar
melhor
os
dados fornecidos no texto.
No
entanto,
a
Física
exige
mais
precisão:
ela
não
se
baseia
em
interpretações
vagas
ou
contextos
implícitos.
Precisamos
de
uma
linguagem
adequada
,
capaz
de
fornecer
todas
as
informações
relevantes
sobre
o
movimento
—
não
apenas
o
valor
da
velocidade,
mas
também
a direção e o sentido
.
É nesse ponto que entra o conceito de
grandeza vetorial,
que será explorado a seguir
Grandeza
Unidade
Símbolo
comprimento
metro
m
massa
quilograma
kg
tempo
segundo
s
velocidade
metro/segundo
m/s

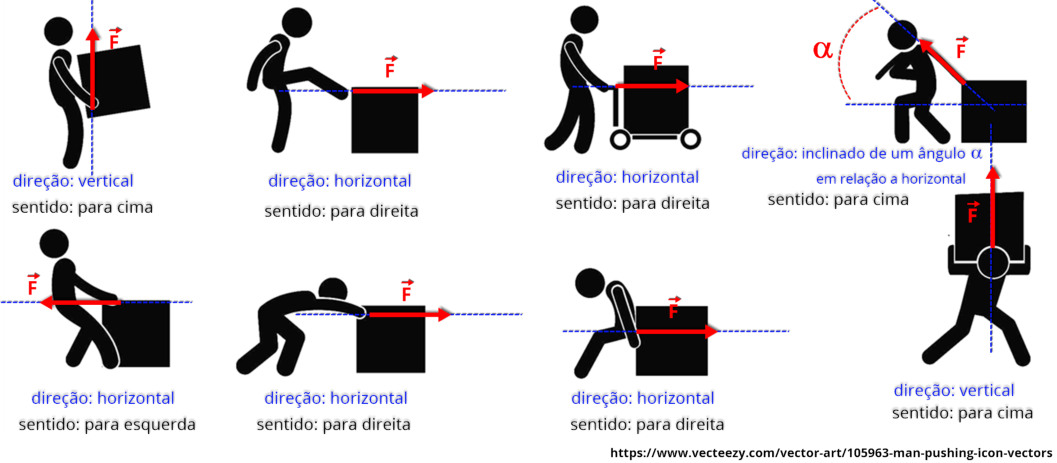
Na
Figura
5
,
apresentamos
diversas
situações
em
que
uma
pessoa
aplica
uma
força
para
empurrar,
carregar
ou
movimentar uma mesma
caixa
.
Embora
a
intensidade
da
força
aplicada
(ou
seja,
seu
módulo
)
seja
a
mesma
em
todos
os
casos,
a
direção
e
o
sentido
dessa
força
variam
—
e
isso,
na
maioria
das
situações
representadas, resulta em
movimentos diferentes da caixa.
Esse
exemplo
evidencia
um
ponto
fundamental:
a
força
é
uma
grandeza
vetorial.
Isso
significa
que,
para
ser
completamente caracterizada, ela deve possuir:
•
Módulo
(intensidade da força),
•
Direção
(linha de ação da força),
•
Sentido
(rumo ao longo da direção).
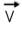
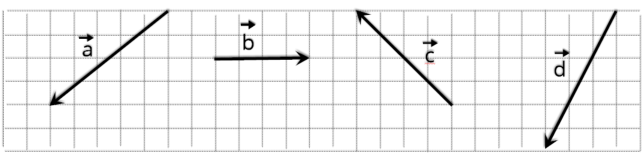
3.0.b Exercício resolvido
R1.
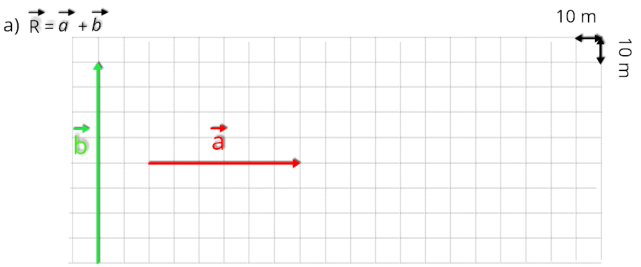
Dê as características dos vetores indicados nas figuras abaixo
Resolução.
Dar a caracterísitica do vetor, significa dizer: o módulo ou intensidade, direção e sentido.
Área
1ª Categoria
2ª Categoria
Mecânica
Eletricidade
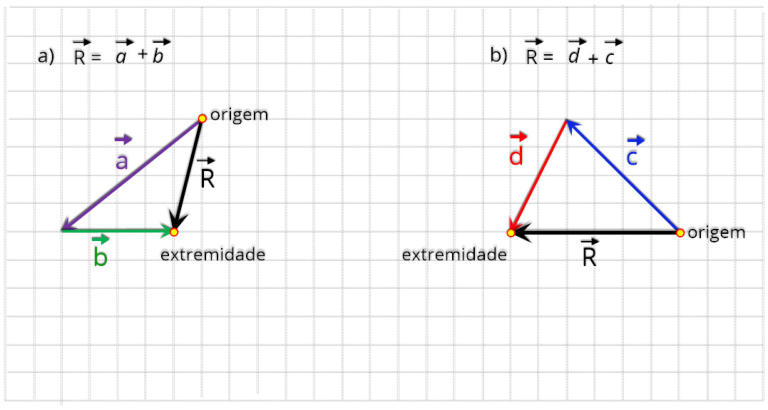
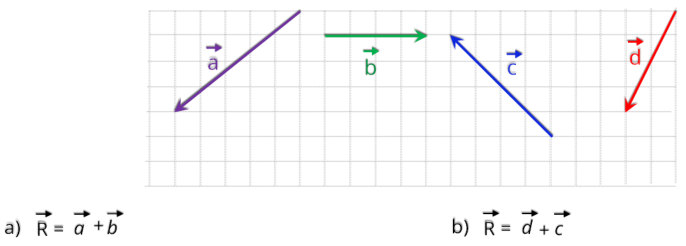
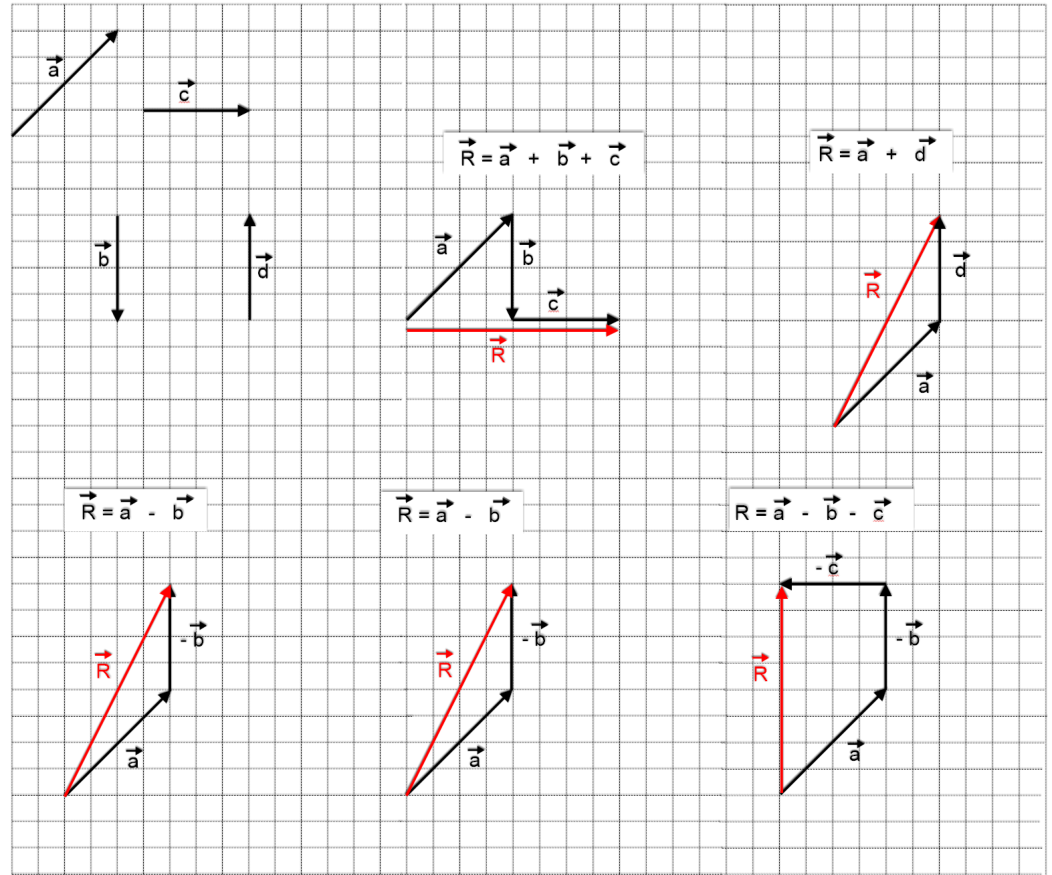
3.0.d Operações com grandezas vetoriais: Soma
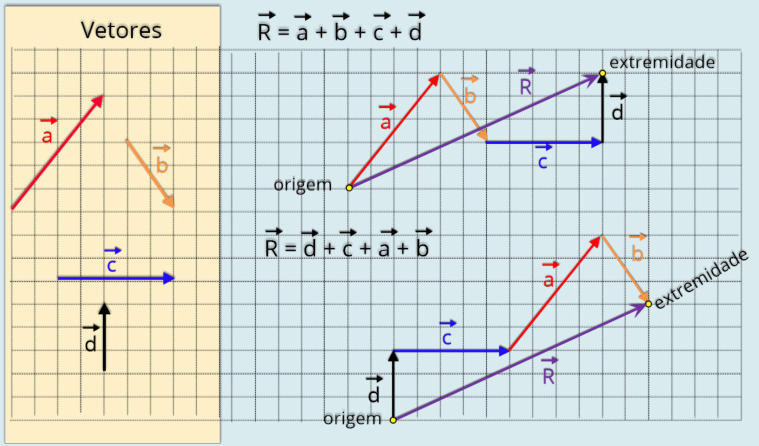
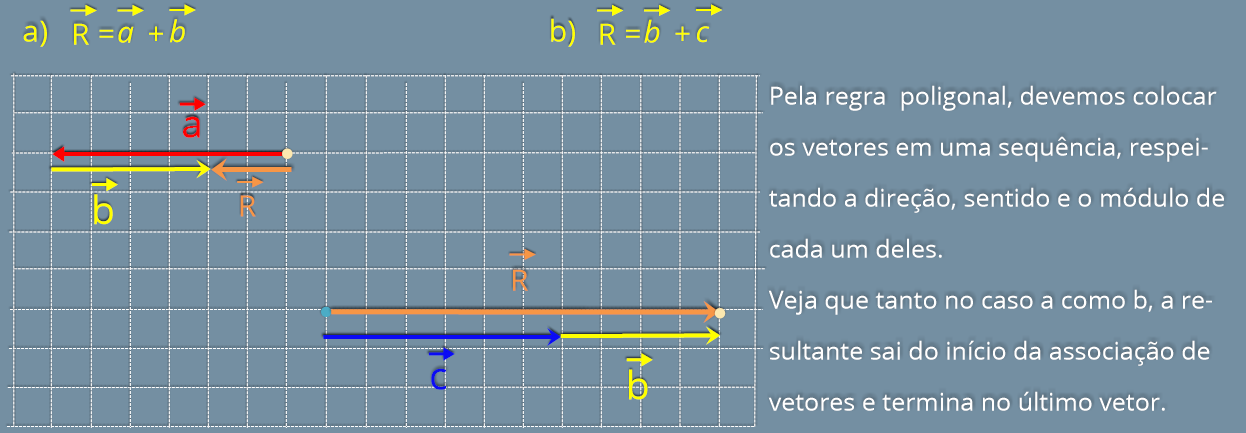
Para realizar a soma podemos utilizar duas maneiras:
Regra
do
polígono
-
Esta
regra
consiste
em
colocar
os
vetores
em
uma
sequência
-
fila
indiana-
,
respeitando
a
direção,
o
sentido
e
o
módulo
de
cada
um
deles.
A
forma
como
colocamos
os
vetores
na
sequência
pode
ser
de
qualquer
forma,
o
resultado
final
será
o
mesmo.
Fizemos
a
soma
adotando duas sequências diferentes de vetores, veja que obtivemos o mesmo vetor resultante.
O
vetor
resultante
é
representado
pelo
segmento
orientado
que
vai
da
origem
do
primeiro
vetor
à
extremidade
do
último.
Esta
forma
de
somar vetores é vantajosa quando desejamos somar um número superior a 2 vetores.
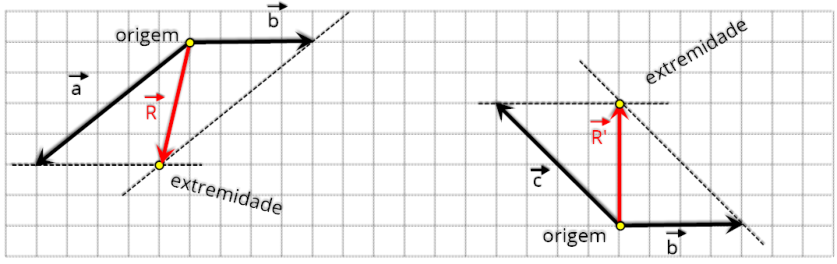
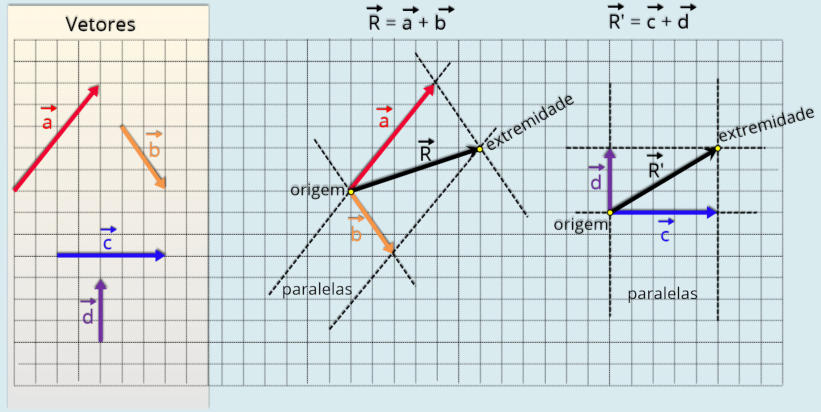
Regra
do
paralelogramo
-
Consideremos
dois
vetores,
como
apresentamos
na
figura
abaixo.
Para
obtermos
a
resultante
destes
vetores
pela
regra do paralelogramo, colocamos a origem dos dois vetores no mesmo ponto (origem).
Em
seguida
traçamos
duas
retas
paralelas
aos
vetores
,
formando
um
paralelogramo.
A
diagonal
do
paralelogramo
corresponde
ao
vetor
resultante como pode ser visto. O mesmo vale para os vetores .
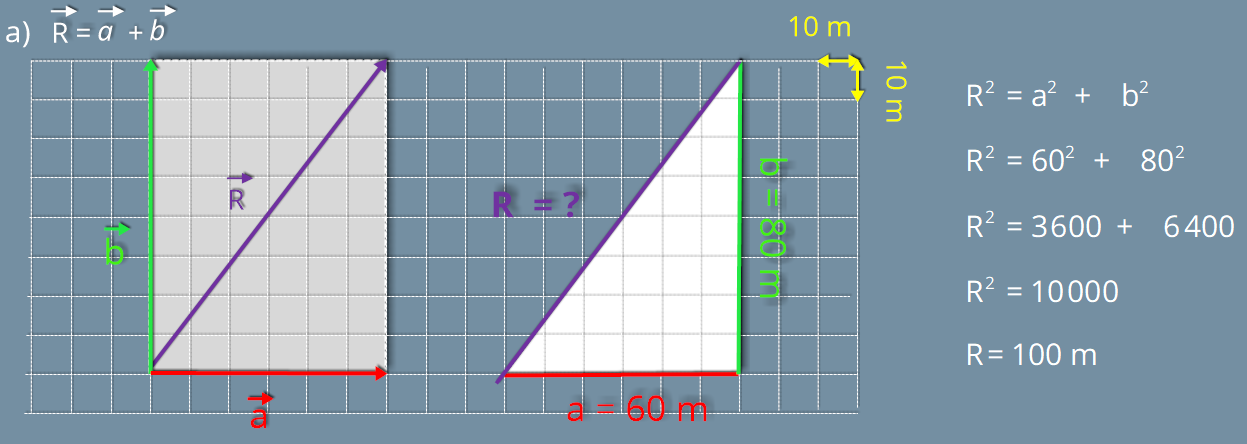
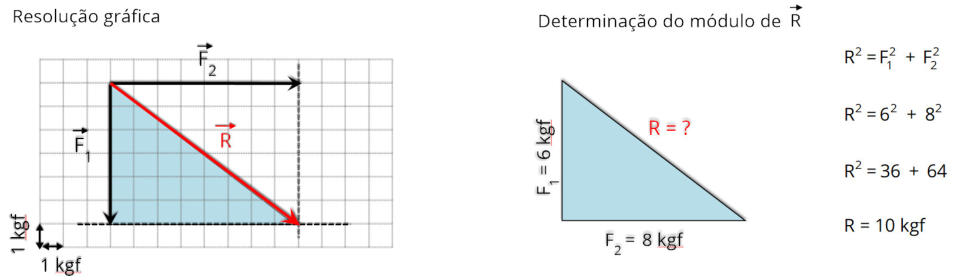
3.0.g Exercícios Resolvidos
R2.
(CESCEM - SP) Qual o módulo da resultante de duas forças de módulo F
1
= 6 kgf e F
2
= 8 kgf que formam entre si um ângulo de 90º ?
Resolução:
Existem
duas
maneira
para
determinar
a
resultante:
pode
ser
graficamente
ou
somente
determinar
o
módulo.
Neste
exercício
bastaria
determinar o módulo, morem mostrarei as duas maneiras.
R3.
Realize a soma vetorial em cada caso a seguir, utilizando a regra do paralelogramo.
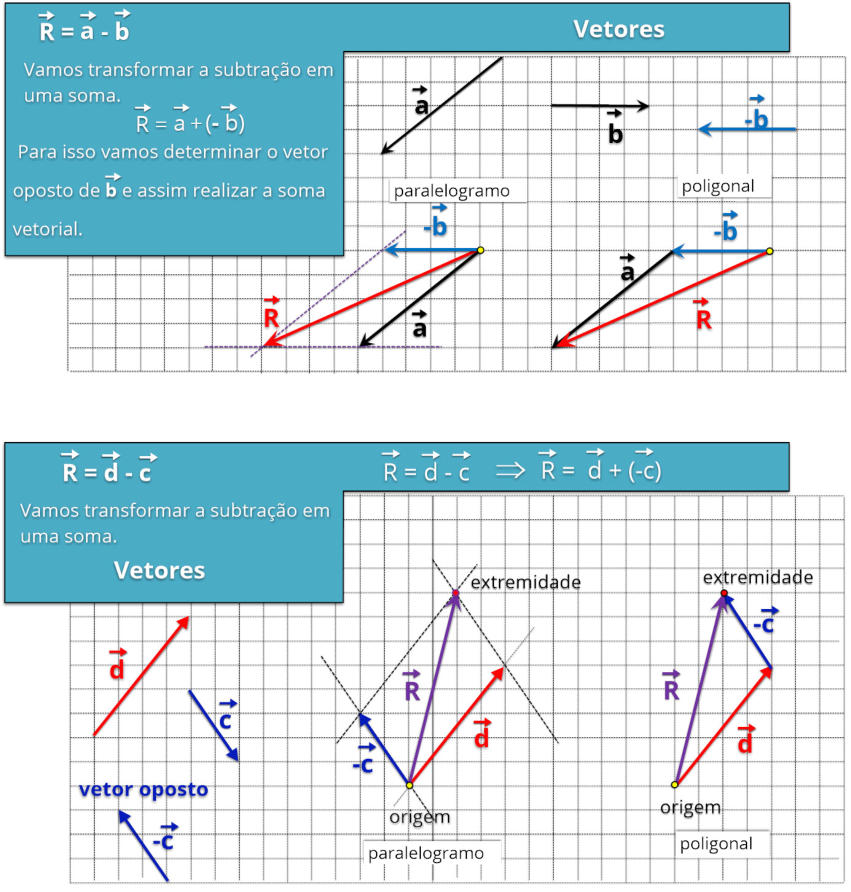
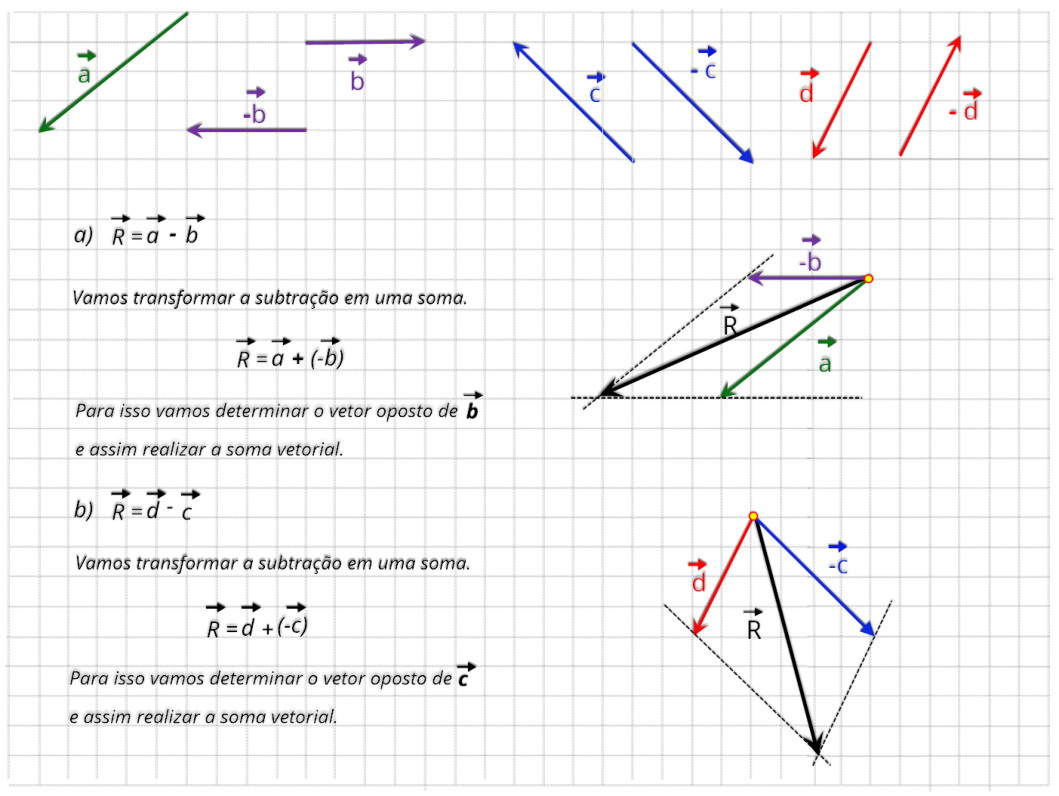
3.0.e Operações com grandezas vetoriais: subtração
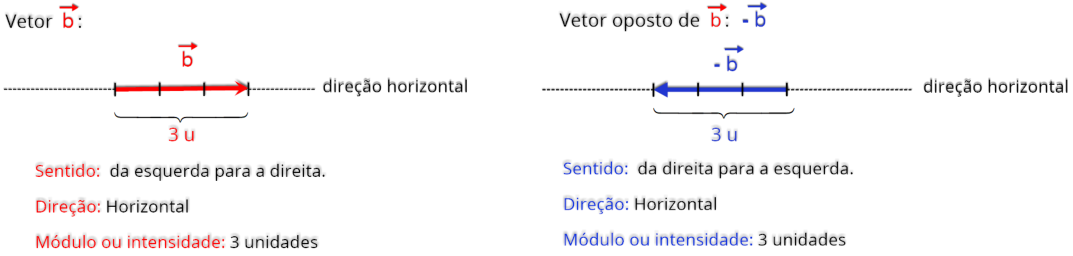
Na
subtração
torna-se
importante
o
conceito
de
vetor
oposto
,
pois
com
ele
podemos
simplificar
a
subtração
de
vetores,
transformando
a
subtração em uma soma de vetores. Vetor oposto é aquele que possui a mesma direção e o mesmo módulo e sentido oposto ao vetor anterior.
Assim
podemos
realizar
a
subtração
de
vetores
transformando
em
soma,
podendo
ser
feito
pela
regra
do
paralelogramo
ou
poligonal
como pode ser visto nos dois exemplos a seguir:
3.0.f Operações com grandezas vetoriais: produto de um vetor por um número real
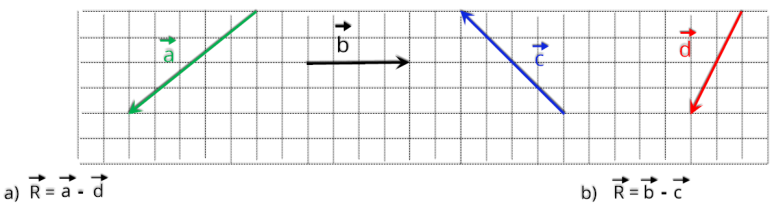
Resolução:
Quando
realizamos
uma
subtração
de
vetores,
é
conveniente
transformar
em
uma
soma
Assim
sendo
vamos
determinar
o
vetor
oposto
de
cada vetor proposto pelo exercício.
R4.
Realize a soma vetorial utilizando a regra poligonal, nos dois casos a seguir.
Resolução:
Para
obtermos
a
resultante
destes
vetores
pela
regra
poligonal,
colocamos
os
vetores
na
sequência
-fila
indiana-
a
partir
da
origem.
Em
seguida,
traçamos a resultante que inicia na origem terminando com a extremidade final.
R5.
Realize
a
soma
vetorial
utilizando
a
regra
do
paralelogramo
ou
poligonal
de
acordo
com
o
que
é
solicitado
em
cada
caso.
Utilize
os
vetores
a
seguir.
Resolução:
Para
obtermos
a
resultante
destes
vetores
pela
regra
do
paralelogramo,
colocamos
a
origem
dos
dois
vetores
no
mesmo
ponto.
Em
seguida,
traçamos
duas
retas
paralelas
aos
vetores,
formando
um
paralelogramo.
A
diagonal
do
paralelogramo
corresponde
ao
vetor
resultante
como
pode ser visto.
Pela regra do paralelogramo:
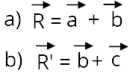
Pela regra poligonal
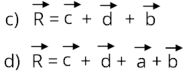
Resolução:
Esta
regra
consiste
em
colocar
os
vetores
em
uma
sequência,
respeitando
a
direção,
o
sentido
e
o
módulo
de
cada
um
deles.
A
forma
como
colocamos os vetores na sequência pode ser de qualquer forma, o resultado final será o mesmo.
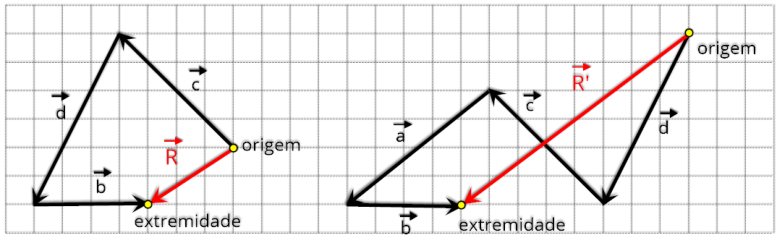
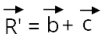
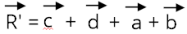
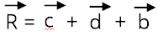
R6.
Realize a soma vetorial utilizando a regra poligonal de acordo com o que é solicitado em cada caso.
3.0.h Exercícios Propostos
P3.
(FAAP-SP)
A
intensidade
da
resultante
entre
duas
forças
concorrentes,
perpendiculares
entre
si,é
de
75
N.
Sendo
a
intensidade
de
uma
força
igual a 60 N, calcule a intensidade da outra.
P4.
Baseando-se
nos
vetores
fornecidos
na
figura
abaixo,
determine
a
intensidade
(ou
módulo)
do
vetor
resultante,
bem
como
a
sua
construção
grafica.
P5.
Determine graficamente o vetor resultante em cada caso indicados na figura abaixo
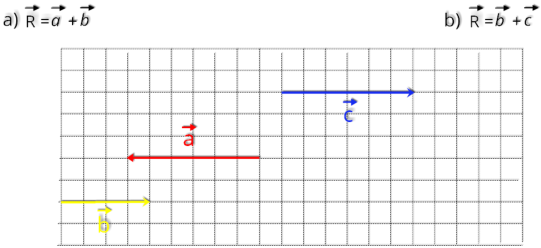
OBS.
A decomposição de vetores faremos quando forem necessárias na mecânica.
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com


Cada
cabo
que
sustenta
as
duas
pontes
da
figura,
pode
ser
entendido
como
um
vetor
força,
a
força
exercida
para
manter
a
ponte
em
equilíbrio,
ele
possui
uma
intensidade
(módulo),
uma
direção e um sentido.

Figura
3
-
Considerando
que
o
marco
zero
ou
origem
dos
espaços
fica
na
cidade
de
São
Paulo,
podemos
afirmar
que
o
veículo
da
figura,
realiza
um
movimento retrógrado (V < 0) , com módulo de 120 km/h, e direção horizontal.
Figura 1 - associação de massas com 5 kg , 2 kg e 1 kg
Na
Figura
1
,
organizamos
três
“pesos”
(massas
usadas
em
balanças)
de
quatro
maneiras
diferentes.
Independentemente
da
forma
como
essas
massas
são
dispostas,
o
valor
total
obtido
será
sempre
8
kg
.
Ou
seja,
por
mais
combinações
que
façamos,
o
conjunto
resultante
mantém
o
mesmo
valor.
Essa
é
uma
informação
completa
sobre
o
sistema
formado
pelas
três
massas:
a
organização
ou
sequência
não
altera
o
resultado final.
Esse
tipo
de
situação
é
um
exemplo
de
grandeza
escalar,
pois
está
completamente
determinado
por
um
valor
numérico
e
uma
unidade
—
no
caso,
8
kg.
O
mesmo
raciocínio
se
aplica
a
outras
grandezas
como
volume,
área,
temperatura,
tempo
,
entre
outras.
Todas
elas
são
grandezas
escalares,
pois
basta
indicar
o
valor
e
a
unidade
para
descrevê-las
plenamente.
Para
saber
mais
sobre
grandezas
na
Física,
clique
aqui
.
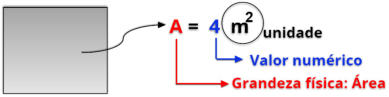

Figura 2
Resumindo o que vimos até agora:
•
Descrição
precisa
dos
fenômenos
:
Muitas
grandezas
físicas
—
como
força,
velo-
cidade
e
aceleração
—
têm
natureza
vetorial.
Ao
utilizarmos
vetores,
conseguimos
repre-sentar
essas
grandezas
de
forma
completa
e
precisa
,
refletindo
fielmente
como
os
fenô-menos
ocorrem
na
prática.
•
Facilidade
nos
cálculos:
As
operações
com
vetores
(como
soma,
subtração
e
mul-
tiplicação
por
escalar)
tornam
os
cálculos
mais
eficientes
e
intuitivos,
principalmente
em
problemas
que
envolvem
várias
grande-
zas vetoriais atuando simultaneamente.
•
Visualização
clara
dos
fenômenos:
A
representação
gráfica
dos
vetores
contribui
para
a
melhor
compreensão
e
visualização
de
situações
físicas
,
mesmo
as
mais
com-
plexas.
•
Aplicação
na
resolução
de
problemas:
Os
vetores
são
ferramentas
essenciais
na
resolução
de
uma
ampla
variedade
de
problemas,
especialmente
em
áreas
como
a
engenharia
. Eles são aplicados, por exemplo,
no cálculo de forças em estruturas como
pontes, ginásios esportivos
ou na análise do movimento de
partículas e corpos em ação.
ciencia-cultura.com
ciencia-cultura.com
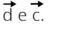
ciencia-cultura.com
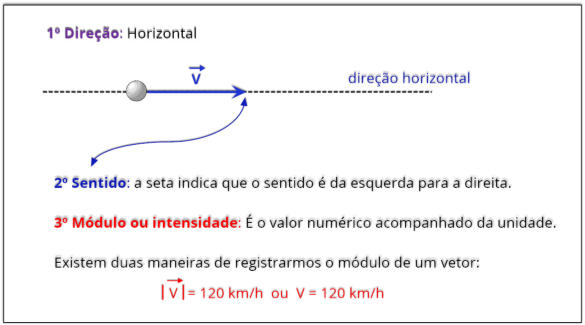
Figura 5


ciencia-cultura.com
Crédito: Pixabay
Crédito: Pixabay

ciencia-cultura.com

ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
3.0.a Vetores
À medida que avançamos no estudo dos movimentos, torna-se cada vez mais importante
descrevê-los utilizando grandezas físicas adequadas. Ao analisarmos um corpo, podemos
identificar diversas de suas características físicas, como a distância percorrida, velocidade, massa,
temperatura, entre outras.
Quando
essas
características
podem
ser
quantificadas
por
meio
de
uma
medida
,
dizemos
que
se
trata
de
uma
grandeza
física
.
Na
tabela
ao
lado,
você
pode
observar
alguns
exemplos
de
grandezas e suas respectivas
unidades de medida
.
Neste capítulo, vamos nos aprofundar nesse tema essencial para o estudo da Física.
A seguir, analisaremos duas situações:
1ª Situação – O conjunto de "pesos" representado na figura abaixo tem uma massa total equivalente a 8 kg...

Nesse caso, apenas o valor
numérico da velocidade e a posição do veículo
são
informações insuficientes.
Para descrever o movimento
de forma completa, precisamos de
mais detalhes.
Esse
tipo
de
situação
exige
o
uso
de
uma
grandeza
chamada
vetorial,
muito
comum
na
Física.
As
grandezas
vetoriais
possuem
três
características fundamentais:
•
Módulo (ou intensidade) —
o valor numérico acompanhado da unidade;
•
Direção —
a linha ao longo da qual a grandeza atua (por exemplo, horizontal, vertical, diagonal);
•
Sentido —
o rumo dentro da direção (por exemplo, para a direita ou para a esquerda, para cima ou para baixo).
Ou
seja,
grandezas
vetoriais
não
apenas
quantificam
algo
,
mas
também
indicam
para
onde
esse
algo
está
se
direcionando.
A
velocidade
é
um
exemplo
clássico
de
grandeza
vetorial,
e
é
com
ela
que
vamos
trabalhar.
Na
Física,
a
velocidade
só
faz
sentido
quando
tratada
como
uma
grandeza vetorial, pois ela descreve tanto a
rapidez do movimento quanto sua direção e sentido
.
No
exemplo
ilustrado
na
Figura
2
,
temos
duas
possibilidades:
o
movimento
pode
estar
se
dirigindo
em
direção
à
cidade
de
São
Paulo
ou
em direção ao interior
. Essa informação —
o sentido do movimento
— é essencial e não pode ser ignorada.
Concluindo:
As
grandezas
vetoriais
são
aquelas
que,
além
do
valor
numérico
(módulo)
e
da
unidade
de
medida
,
também
precisam
da
direção
e
do
sentido
para serem completamente definidas.
Para
um
movimento
ao
longo
de
uma
rodovia,
a
velocidade
pode
assumir
valores
positivos
ou
negativos
,
dependendo
do
sentido
do
deslocamento
.
Chamamos
de
movimento
progressivo
quando
o
deslocamento
ocorre
no
mesmo
sentido
da
orientação
da
trajetória
,
e
nesse
caso,
a
velocidade
é
considerada
positiva
.
Por
outro
lado,
se
o
deslocamento
ocorre
em
sentido
contrário
à
trajetória
,
temos
um
movimento
retrógrado
, e a velocidade será
negativa
.
No
nosso
exemplo
da
Figura
3,
um
veículo
que
se
desloca
do
interior
com
o
sentido
à
cidade
de
São
Paulo
está
indo
contra
a
orientação
da
rodovia
,
portanto,
sua
velocidade
será
negativa
.
Já
um
veículo
que
segue
de
São
Paulo
no
sentido
ao
interior
estará
em
movimento
progressivo
, com
velocidade positiva
.
Lembre-se:
nas
rodovias
do
estado
de
São
Paulo,
o
marco
zero
está
localizado
na
capital.
A
numeração
dos
quilômetros
aumenta
à
medida
que
nos afastamos da cidade de São Paulo, rumo ao interior.
O movimento ilustrado na
Figura 3
pode ser representado por um
vetor velocidade
, que possui três características fundamentais:
•
Direção
(ao longo da rodovia),
•
Sentido
(interior
→
capital ou capital
→
interior),
•
Módulo
(o valor da velocidade em km/h).
Essa representação vetorial está mostrada na
Figura 4
.
Observe que a forma de distinguir uma
grandeza vetorial
de uma
grandeza escalar
é a
notação com uma seta sobre o símbolo da grandeza.
Por exemplo:
m
representa a
massa
(grandeza escalar);
representa a
velocidade vetorial
(grandeza vetorial).
Figura 4
Portanto,
não basta saber o quanto de força
foi aplicado; é essencial saber também como e para onde ela foi aplicada.
Direção
(linha de ação da força),
Sentido
(rumo ao longo da direção).
Portanto,
não basta saber o quanto de força foi aplicado;
é essencial saber também
como
e
para onde ela foi aplicada.




Cinemática









