



© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física
2.3 Gráficos do Movimento Retilíneo Uniforme

Cinemática

Corrida Nascar
Veja
alguns
passos
importantes
que
você
deve
realizar para a leitura de um gráfico:
1ª
informação:
O
gráfico
é
uma
reta,
o
que
significa
que
a
função
é
representada
por
uma
equação
do
1º
grau.
Na
cinemática
uma
equação
deste tipo representa o movimento uniforme,
s = s
0
+ v.t.
2ª
informação:
A
reta
inicia
no
eixo
dos
espaços
(s)
em
s
0
=
4
m
,
sendo
a
posição
onde
dá
início
o
movimento
.
3ª informação:
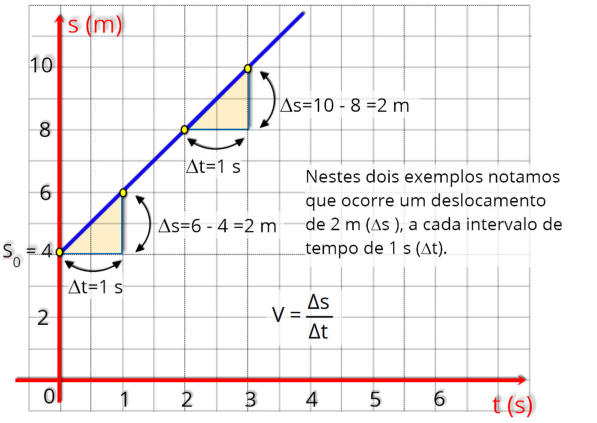
Para que saibamos determinar o
Olhando
o
gráfico
onde
os
dados
das
posições
estão
representados
no
eixo
s
(m)
,
e
o
tempo
indicados
no
eixo
t
(s),
nos
fornece
uma
representação
visual do movimento.
A
razão
entre
o
espaço
percorrido
pelo
tempo
empregado, é a velocidade do corpo.
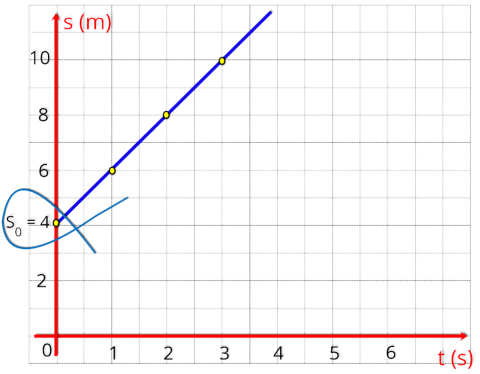
No nosso exemplo a velocidade é:
V = 2 m/s
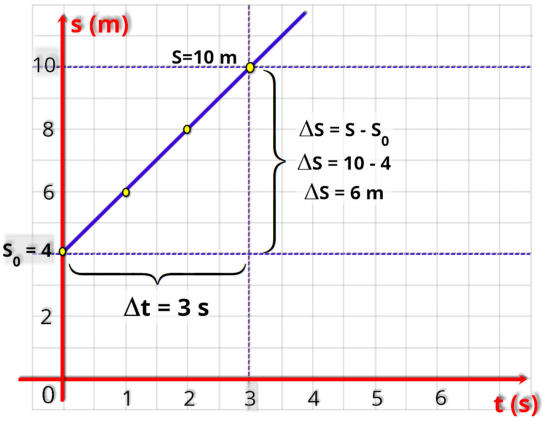
Outra
forma
de
determinar
a
velocidade,
é
escolher
dois
pontos
na
reta,
como
mostramos
no
gráfico
ao
lado.
Escolhemos
a
posição
inicial
S
0
=
4
m
e
a
posição
final
do
grafico
que
é
S
=
10
m.
Como
mostramos
ao
lado
o
espaço
percorrido
é
D
s
=
6
m
e
m
um
intervalo
de tempo onde
D
t = 3 s.
Da
mesm
forma
que
fizemos
antes,
obteremos
o
valor da velocidade.

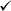


2.3.b Como construímos o gráfico?
A
partir
da
origem
dos
eixos
x
e
y,
marcamos
os
valores
do
tempo
no
eixo
x
(
das
abcissas)
-
variável
independente
-
que
agora
chamaremos
de
eixo
do
tempo
(
t
)
.
Em
seguida
marcaremos
no
eixo
y
(das
ordenadas)
-
variável dependente
-, que agora chamaremos de eixo dos espaços
( s )
.
Alguns cuidados que devem ser tomados ao construir um gráfico:
Os
dois
eixos
são
independentes
um
do
outro,
pois
representam
grandezas
físicas
diferentes:
um
a
grandeza
tempo
e
o
outro
a
grandeza
espaço
.
O
tamanho
dos
intervalos
em
cada
eixo,
depende
unicamente
do
“tamanho”
da
folha
que
temos
para
construir
o
gráfico e do bom senso.
Quando
definimos
os
intervalos
em
que
vamos
dividir
os
eixos,
estamos
construindo
uma
escala
para
os
espaços
e
uma
escala
para
o tempo. Construídas as escalas, colocam-se os pontos no gráfico.
O resultado obtido pode ser visto na figura ao lado. A tabela, o desenho
da trajetória e o gráfico são formas de representação da equação horária
de posição em função do tempo, que no nosso caso é:
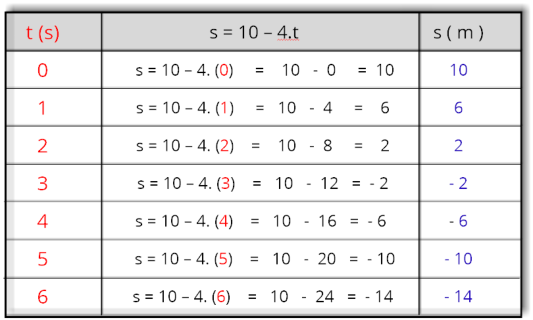
s = 10 - 4.t
A
velocidade
é
constante
e
neste
exemplo
é
V
=
-
4
m/s,
o
que
caracterisa
um
movimento
retrógrado.
O
movimento
retrógrado
é
aquele
em
que
o
corpo
se
desloca
no
sentido
oposto
ao
da
orientação
da
trajetória,
e
a
indicação
de
que
o
movimento
é
retrógrado
é
dado
pela
velocidade negativa.
2.3.d Interpretando um gráfico s x t
Agora
que
sabemos
construir
um
gráfico,
faremos
o
caminho
inverso,
ou
seja,
dado
um
gráfico
dos
espaços
(s)
pelo
tempo
(t),
montaremos
a
sua
equação horária. Como exemplo veja o gráfico abaixo:
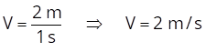
2.3.a Introdução - A Importância dos Gráficos no MRU.
Os
gráficos
são
ferramentas
poderosas
na
física,
especialmente
quando
se
trata
de
analisar
movimentos.
No
caso
do
Movimento
Retilíneo
Uniforme
(MRU),
onde
a
velocidade
é
constante
e
a
trajetória
é
uma
linha
reta
,
os
gráficos
nos
oferecem
uma
visualização
clara
e
a
compreensão das relações entre as grandezas físicas envolvidas, como
posição (S)
,
velocidade (V)
e
tempo (t).
Vantagens que os gráficos nos dão:
Representação visual:
Os gráficos transformam equações matemáticas em imagens, facilitando a compreensão do movimento.
Identificação
de
características:
Através
dos
gráficos,
podemos
identificar
rapidamente
características
como:
Velocidade,
Sentido
do
movimento e a
posição inicial (S
0
)
.
Tipos de gráficos do MRU:
Gráfico da posição (s) em função do tempo (t):
Uma reta com inclinação constante.
Gráfico da velocidade (v) em função do tempo (t)
: Uma reta horizontal, pois a velocidade é constante.
Vamos
iniciar
pelo
gráfico
da
posição(s)
em
função
do
tempo
(t).
Vimos
na
aula
anterior
que
a
equação
que
descreve
o
movimento
retilíneo
uniforme é dada por:
Da
matemática
sabemos
que
a
equação
dos
espaços
do
Movimento
Retilíneo
Uniforme
é
uma
equação
do
1º
grau
o
que
resulta
em
uma
reta.
Para
ilustrar
o
que
estamos
falando,
vamos
construir
um
gráfico
com
a
seguinte
equação:
s
=
10
-
4.t
no
sistema
internacional
(SI).
Inicialmente vamos montar uma tabela, onde atribuiremos valores ao tempo, e teremos a posição,veja como fica:





Observação:
Na
Cinemática
os
valores
para
o
tempo
são
positivos,
não
trabalhamos com tempo negativo.
Qualquer
valor
que
seja
atribuido
ao
tempo
nos
dará
o
mesmo
gráfico,
no
entanto
não
vamos
nos
complicar,
utilizaremos valores fáceis como: 0 s, 1 s, 2 s, 3 s , . . . .
Isto
quer
dizer
que
se
você
considerar
mais
fácil
outros
valores, utilize então.





Se
quisermos
visualizar
como
ficaria
o
movimento
em
uma
trajetória,
dê
uma
olhada
na
figura
abaixo.
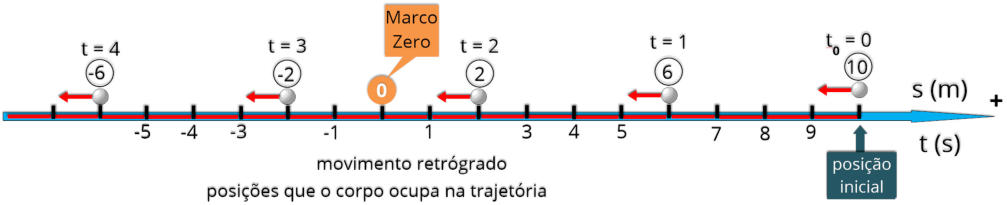
No
instante
inicial
(t
0
=
0),
o
corpo
se encontra na posição s
0
= 10 m, a cada instante ele se move no sentido contrário ao da trajetória, ou seja um movimento retrógrado ( V < 0 ).
s = 10 - 4.t



Reta
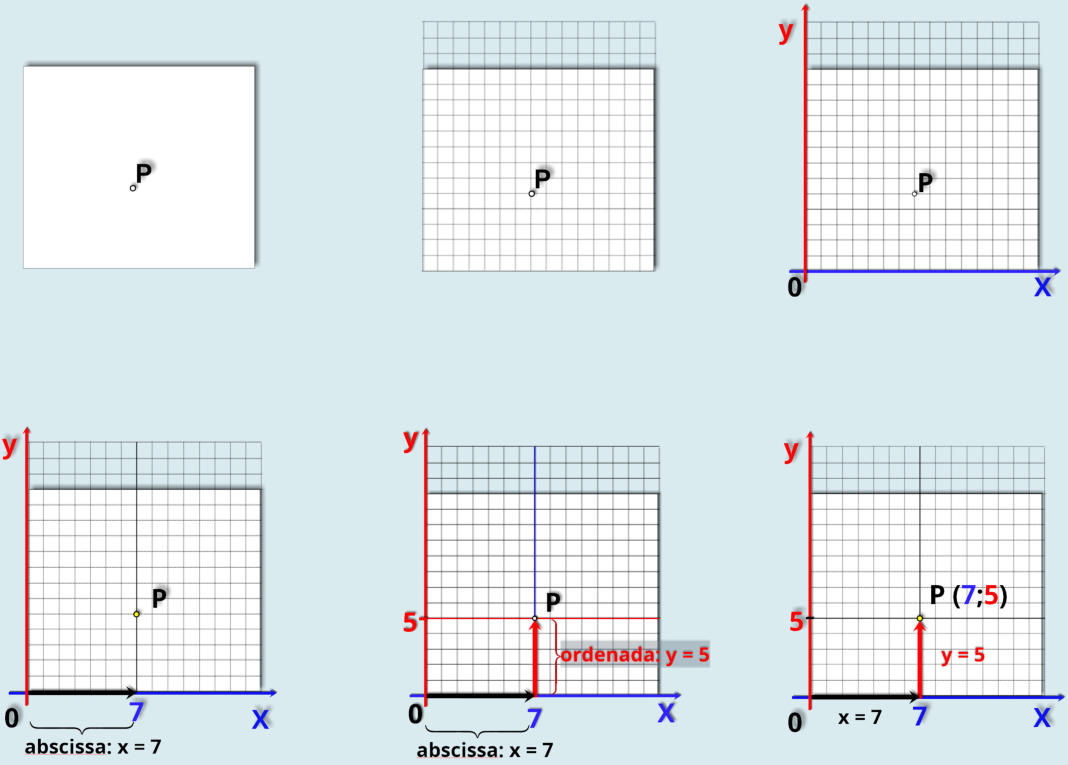
2.3.c O Plano cartesiano
O
primeiro
passo
para
aprendermos
como
se
constrói
um
gráfico,
é
saber
localizar
um
ponto
em
um
plano.
Na
figura
1,
indicamos
o
ponto
P.
Não
é
possivel
nestas
condições
afirmar
qual
é
a
sua
posição
dentro
do
plano
“branco”,
assim
nasce
à
necessidade
de
criarmos
regras
para dar a sua localização
Unidades do Sistema Internacional (SI)
posição - s
metro (m)
velocidade - V
metro/segundo (m/s)
tempo - t
segundo (s)
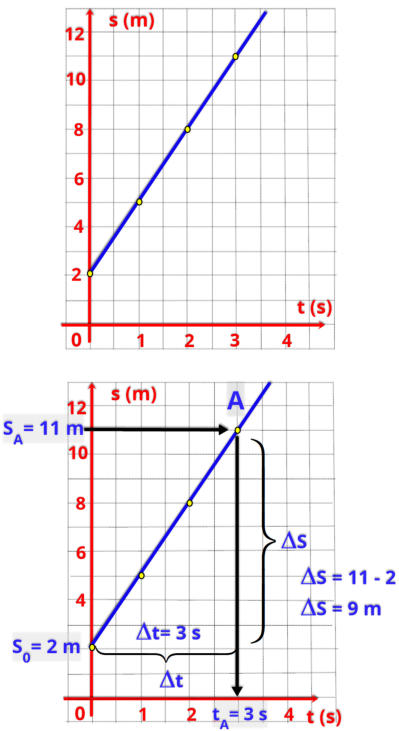
1º Exemplo
2º Exemplo
Escreva a equação horária do gráfico abaixo.

Escrever a equação horária significa obter algumas informações do gráfico!
O
gráfico é uma reta,
o que significa que a função é representada por uma equação do 1º grau. Neste caso, o movimento é uniforme,
S = S
0
+ v.t.
Vamos determinar a
velocidade V,
e a
posição inicial S
0
.
Na
figura 2
, a reta inicia na
posição S
0
= 2 m,
agora vamos determinar a velocidade.
Para determinar a velocidade vamos escolher dois pontos na reta, qualquer ponto. Eu vou escolher o ponto A.




Fig. 1
Fig. 2
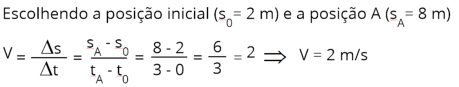
A função horária fica: s = 2 + 2.t
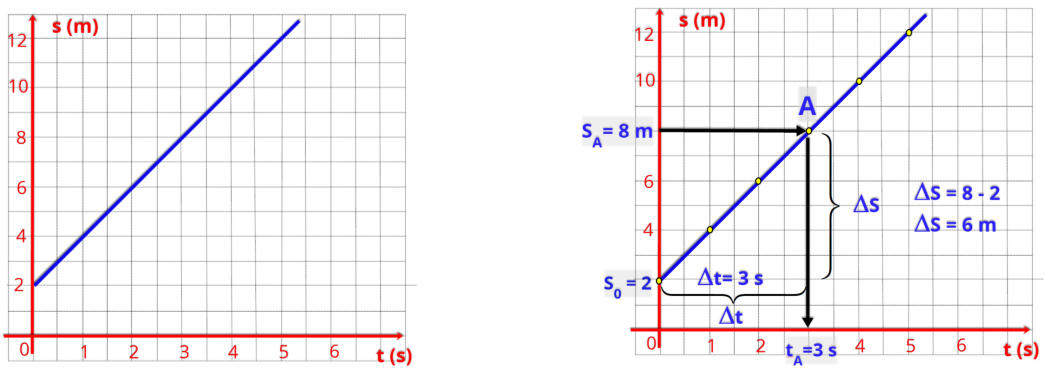
3º Exemplo
Vamos determinar a equação horária,
s = s
0
+ v.t.
O
gráfico
é
uma
reta,
o
que
significa
que
a
função
é
do
1º
grau,
ou seja, é um movimento uniforme.
Vamos determinar a
velocidade V,
e a
posição inicial S
0
.
Na
figura 2
, a reta inicia na
posição inicial S
0
= 2 m.
Para
a
velocidade
vamos
escolher
dois
pontos
na
reta,
a
posição
inicial e a posição A.




Esreva a equação horária do gráfico abaixo.
Figura 1
Figura 2
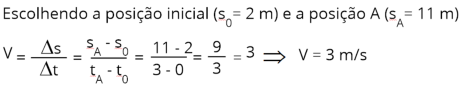
Na
vertical,
nos
deslocamos
em
direção
ao
ponto
P,
caminhando
5
unidades
ou
5
quadrados, que significa dizer que y = 5.
Ao
nos
deslocarmos
pelo
eixo
das
abscissas,
partindo
da
origem,
verifica-
mos que o nosso deslocamento é de
x = 7 unidades.
O
ponto
P,
fica
determinado
pela
sua
abscissa
e
pela
sua
ordenada,
o
qual
chamamos
de
coordenadas
do
ponto
P.
No
plano
cartesiano,
primeiro
o
avanço
horizontal (x) e depois o vertical (y).
P (abscissa ; ordenada ) = P ( x ; y ) = P ( 7; 5 )
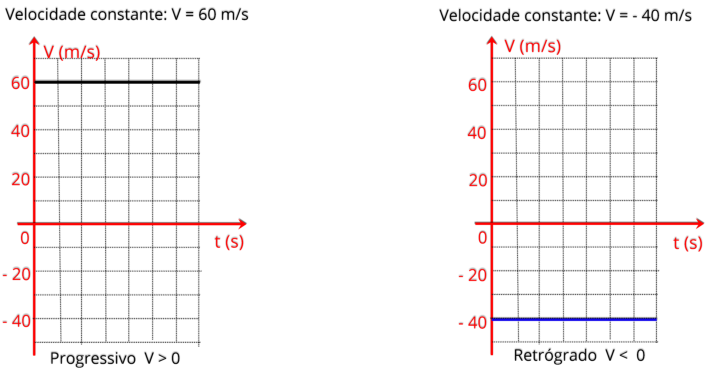
2.3.e Interpretando um gráfico v x t
Sabemos
que
no
movimento
retilíneo
uniforme
a
velocidade
é
constante,
portanto
o
gráfico
será
uma
reta
paralela
ao
eixo
dos
tempos,
como
pode ser visto nos dois exemplos a seguir:
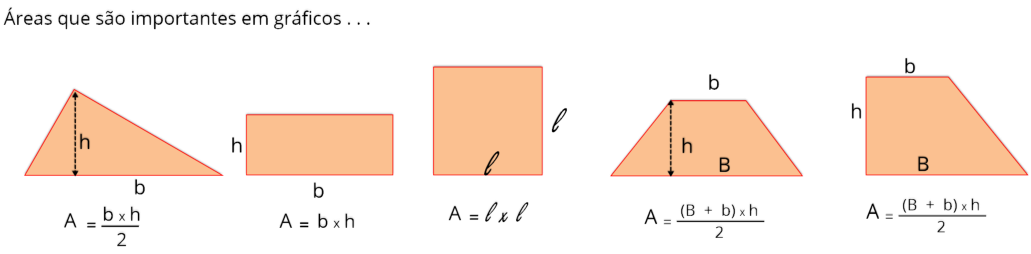
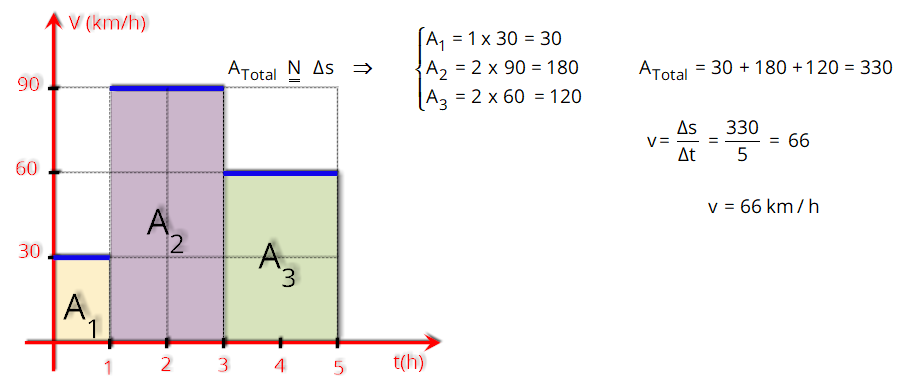
A
informação
que
podemos
obter
do
gráfico
da
velocidade
pelo
tempo
(V
x
t)
é
o
espaço
(
D
s)
que
o
corpo
sofre
em
um
intervalo de tempo.
O
espaço
pode
ser
obtido
encontrando
a
área
da
figura
formada
entre
a
reta
da
velocidade
com
o
eixo
dos
tempos
(t).
O
valor
numérico
da
Área
da
figura
corresponde
ao
espaço
percorrido
num
certo intervalo de tempo.
2.3.f Exercícios resolvidos
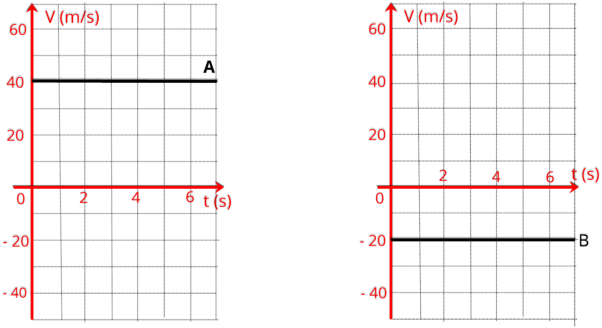
R1.
Determine
para
os
moveis
A
e
B
a
variação
de
espaço
entre
os
instantes
0
e
4
s.
São dados os gráficos da velocidade escalar em função do tempo.
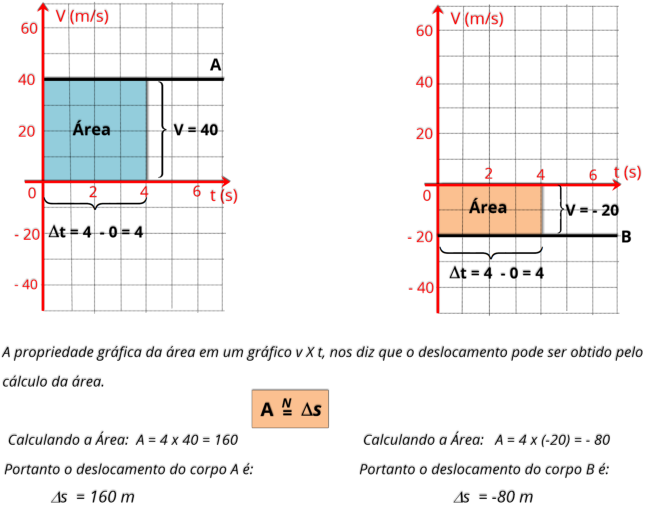
Resolução:
De acordo com o que é solicitado no exercício, vamos indicar nos dois gráficos qual é o
intervalo de tempo entre 0 s e 4 s.
R2.
(EE
São
Carlos-SP)
O
gráfico
ao
lado
representa
o
espaço
(s)
no
movimento
de
um
homem,
em
função do tempo. Qual a velocidade escalar do homem:
a)
para t = 5,0 s;
Resolução
a)
para t = 5,0 s.
Resolução:
A velocidade no intervalo de tempo em que ocorre um movimento uniforme é:
b)
para t = 20 s.
Resolução:
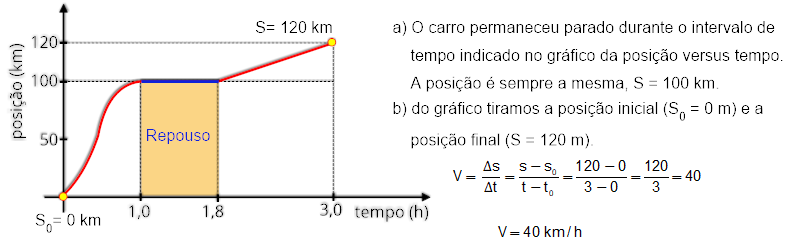
No instante t = 20 s verificamos pelo gráfco, que o corpo não muda de posição, significando que ele está em repouso.
A velocidade é: V = 0 m/s.
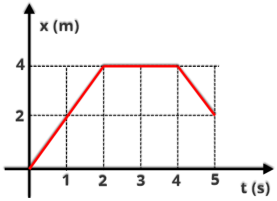
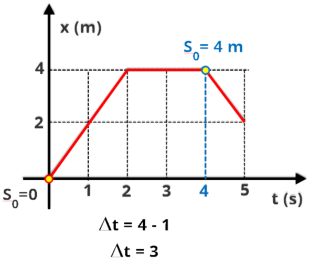
R3.
(UFPE
1996)
O
gráfico
a
seguir
representa
a
posição
em
função
do
tempo
de
um
objeto
em
movimento
retilíneo.
Qual
a
velocidade
média
do
objeto,
em
m/s,
correspondente
aos
primeiros
quatro segundos?
Resolução
Inicialmente
vamos
indicar
o
intervalo
de
tempo
e
o
deslocamento
do
corpo
através
do
gráfico,
como pode ser visto abaixo.
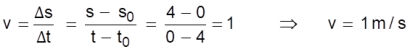
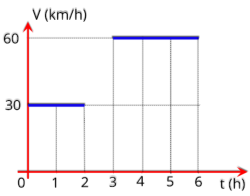
2.3.8 Exercícios propostos
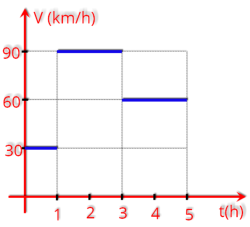
P1.
(UFCE
-
1986)
Um
automóvel
move-se
numa
estrada
conforme
o
gráfico
v
x
t
na
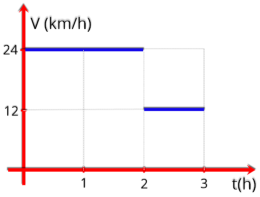
figura abaixo. Determine sua velocidade média, em km/h, após 5 h.
P2.
O
gráfico
abaixo
representa
a
velocidade
de
um
ciclista
em
função
do
tempo,
num
determinado percurso. A
velocidade média do ciclista foi, em km/h:
P3.
Um
automóvel
faz
uma
viagem
em
6
horas
e
sua
velocidade
varia
em
função
do
tempo
aproximadamente
como
mostra
o
gráfico
abaixo.
Determine
a
velocidade
média do automóvel durante a viagem.
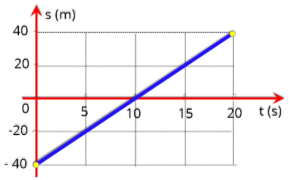
P4.
O
gráfico
abaixo
representa
o
espaço
de
um
ponto
material
em
movimento
como
uma função do tempo. Escreva a correspondente
equação horária do movimento.
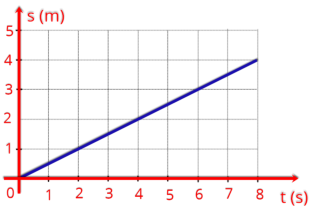
P5.
Considere
um
movimento
cuja
posição
s,
em
função
do
tempo
t,
está
representada
no
gráfico.
Determine
o
espaço
percorrido
pelo
móvel
entre
os
instantes
t = 0 s e t = 20 s, em metros.
P6.
(Ufpr
2020)
Um
objeto
moveu-se
ao
longo
de
uma
linha
reta
e
um
observador
inercial
mediu
sua
posição
nessa
linha,
em
função
do
tempo
elaborando
o
gráfico
a
seguir. O objeto tem uma massa constante m = 25 g.
Com base nos dados apresentados:
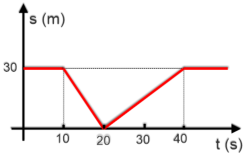
a) Calcule o deslocamento do objeto entre os instantes t = 0 s e t = 4 s.
b) Determine a velocidade do objeto no instante t = 5 s.
c) Obtenha a energia cinética do objeto no instante t = 2 s.
P7.
(UFRJ
2005)
A
posição
de
um
automóvel
em
viagem
entre
duas
cidades
foi
registrada
em
função
do
tempo.
O
gráfico
a
seguir
resume
as
observações
realizadas
do início ao fim da viagem.
a) Indique durante quanto tempo o carro permaneceu parado.
b) Calcule a velocidade escalar média do carro nessa viagem.
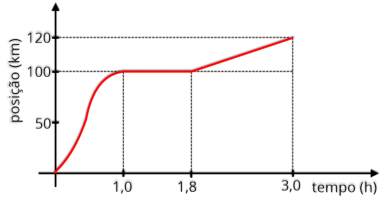
P8.
(UDESC
-
1996)
A
posição
de
um
corpo
varia
em
função
do
tempo,
de
acordo
com
o
gráfico
a
seguir.
Determine,
DESCREVENDO
passo
a
passo,
os
raciocínios
adotados
na
solução
das
questões
adiante:
a) a posição do corpo no instante 5 segundos;
b) a velocidade no instante 15 segundos;
c) a posição no instante 25 segundos.
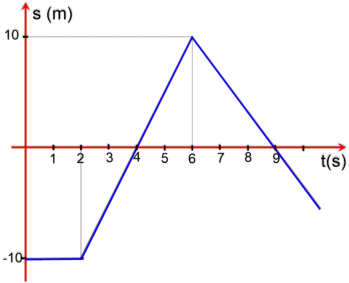
P9.
(
ESAL
–
MG)
As
posições
de
um
ponto
material
variam,
em
função
do
tempo,
de
acordo com o gráfico abaixo.
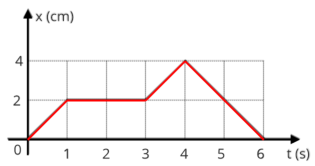
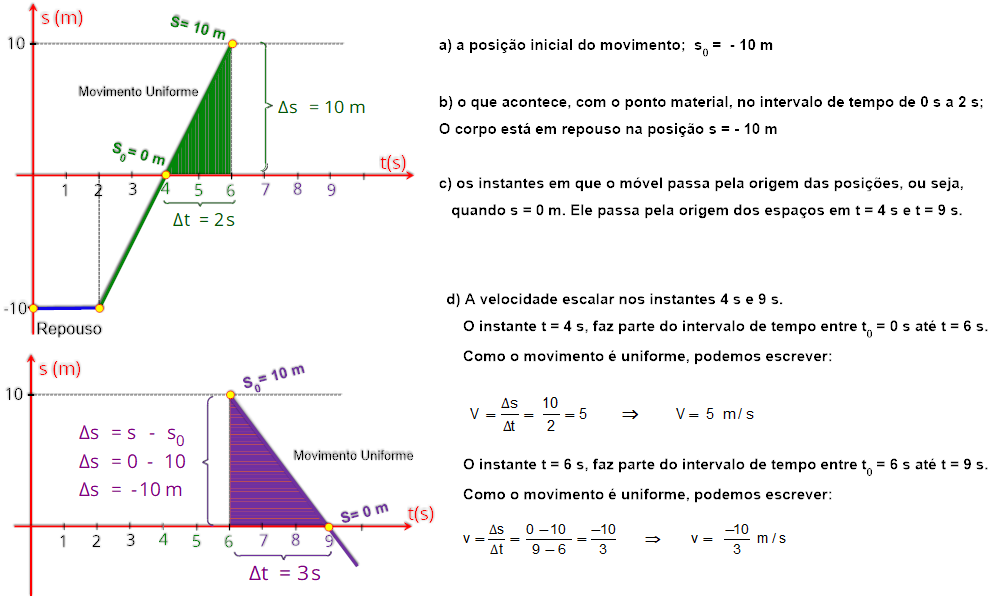
Determine:
a) a posição inicial do movimento;
b) o que acontece, com o ponto material, no intervalo de tempo de 0 a 2s;
c) os instantes em que o móvel passa pela origem das posições;
d) a velocidade escalar nos instantes 4s e 9s.
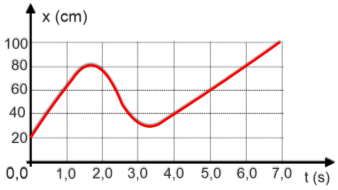
P10.
(UFPE
2003)
O
gráfico
descreve
a
posição
x,
em
função
do
tempo,
de
um
pequeno
inseto
que
se
move
ao
longo
de
um
fio.
Calcule
a
velocidade
do
inseto,
em
cm/s, no instante t = 5,0 s.
2.3.9 Testes propostos
T1.
(Espcex
2020)
Considere
um
objeto
que
se
desloca
em
movimento
retilíneo
uniforme
durante
10
s.
O
desenho
abaixo
representa
o
gráfico
do
espaço
em
função
do tempo. O espaço do objeto no instante t = 10 s em metros, é
a) 25 m
b) 30 m
c) 33 m
d) 36 m
e) 40 m
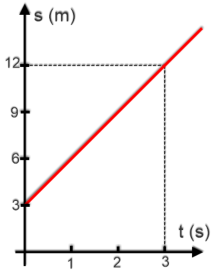
T2.
(ifsul
2018)
Uma
partícula
realizou
um
movimento
unidimensional
ao
longo
de
um
eixo
0X
e
o
comportamento
da
sua
posição
x,
em
função
do
tempo
t,
foi
representado
em um gráfico, ilustrado na figura ao lado.
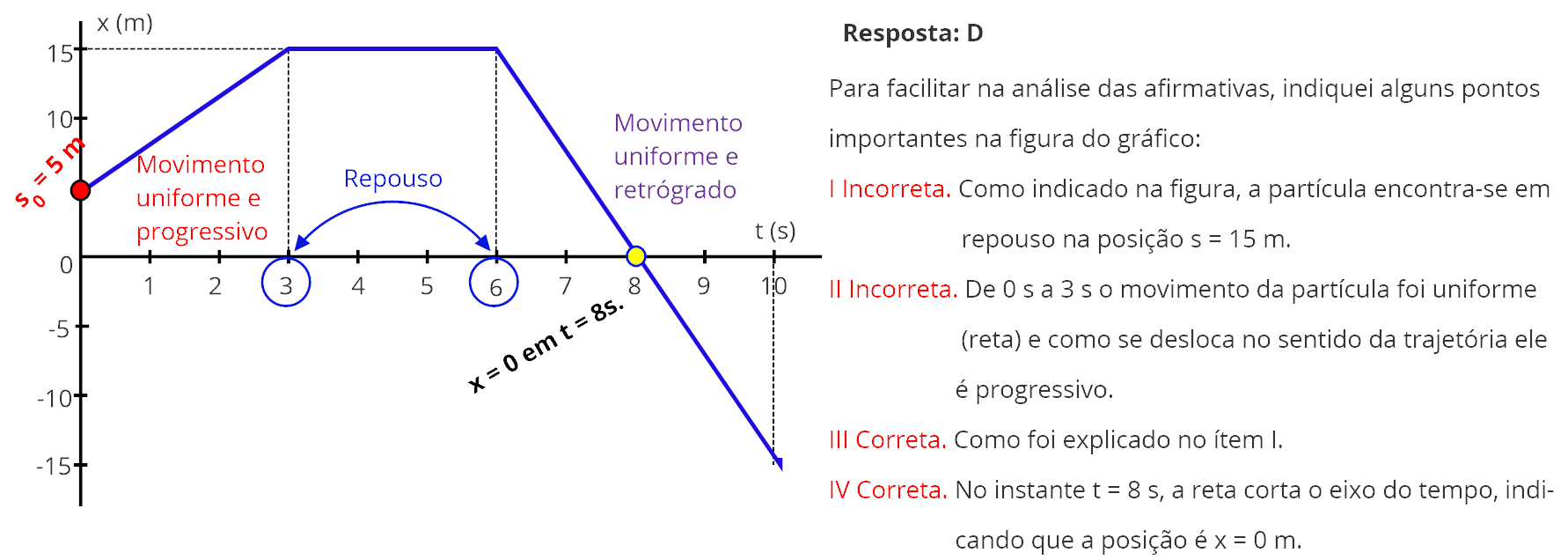
Analise as seguintes afirmativas referentes ao movimento realizado por essa partícula:
I. Entre os instantes 3 s e 6 s, a partícula realizou um movimento uniforme.
II. Entre os instantes 0 s e 3 s, a partícula realizou um movimento acelerado.
III. Entre os instantes 3 s e 6 s, a partícula estava em repouso.
IV. No instante 8 s, a partícula estava na origem do eixo x.
Estão corretas apenas as afirmativas
a) I e II. b) I e IV. c) II e III. d) III e IV.
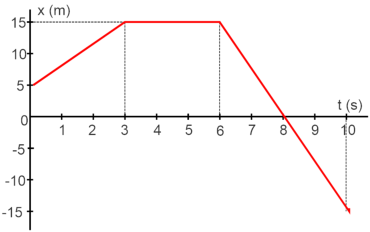
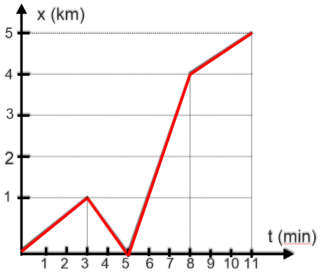
T3.
(Pucrj
2016)
Um
carro
saiu
da
posição
x
=
0
km
até
seu
destino
final
em
x
=
5
km
de
acordo
com
gráfico
x
(km)
x
t
(min)
mostrado
na
figura.
Finalizado
o
percurso,
o
computador
de
bordo
calcula
a
velocidade
escalar
média
do
carro,
sem
considerar
o
sentido do movimento.
Qual é esta velocidade escalar média dada pelo computador, em
a) 27 b) 33 c) 38 d) 47 e) 60


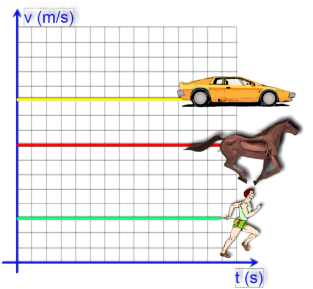
O
movimento
é
chamado
uniforme
quando
a
velocidade
for
constante.
Quanto
maior
a
velocidade,
mais
alto
se
localiza
a
reta
(carro).
Se
a
reta
se
aproxima
do
eixo
x,
sua
velocidade se aproxima do zero.
(Gráfico fora de escala)
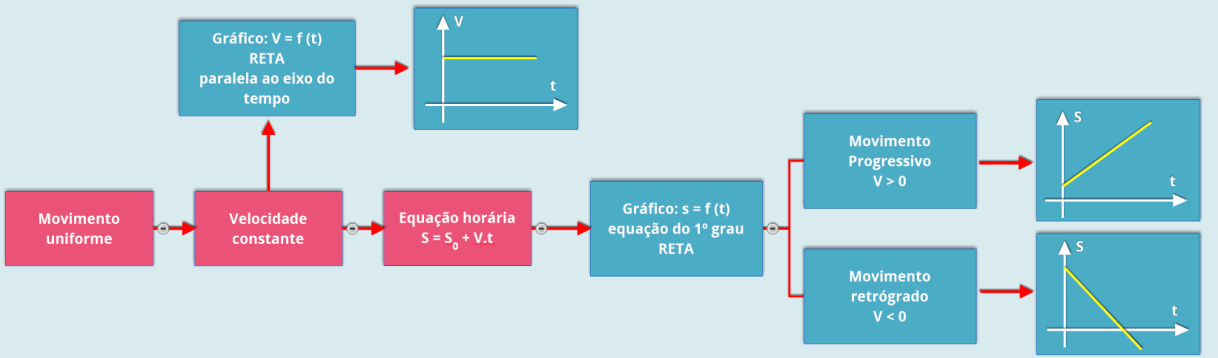
2.3.g Mapa conceitual
Este
mapa
conceitual
apresenta
uma
visão
geral
dos
exemplos
e
conceitos
vistos
nesta
página,
ele
se
apresenta
na
forma
de
um
conjunto
de
proposições
interconectadas.
O
significado
de
qualquer
conceito
é
a
soma
de
todas
as
ligações
que
contêm
o
conceito.
Para
"ler"
o
mapa
conceitual, comece do Movimento Uniforme, e vá até os itens mais específicos e os exemplos nas partes mais externas.
Procure fazer o teu mapa conceitual, vai te ajudar a organizar os conceitos desta lição.




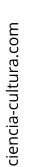
Se
o
plano
for
quadriculado,
o
nosso
trabalho
na
localização
do
ponto
P
fica
mais
fácil.
Observe
como ficou a figura.
Vamos
determinar
a
distância
de
P
em
relação
a
dois
eixos
que
se
cruzam
perpendicularmente,
onde
o
horizontal
chamamos
de
eixo
das
abscissas
(eixo
x),
e
o
da vertical eixo das ordenadas (eixo y).
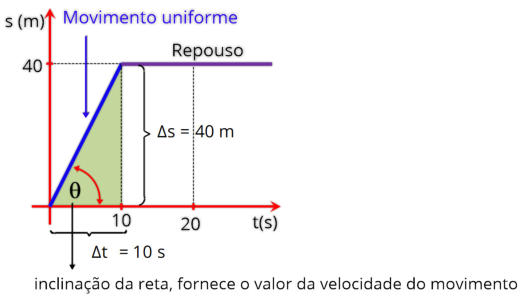
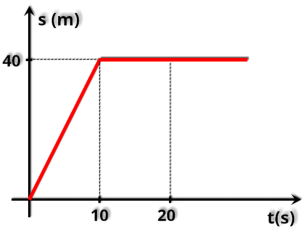
Inicialmente
vamos
interpretar
o
gráfico.
É
possivel
verificar
que
o
gráfico
pode
ser
dividido
em
duas
partes,
do
instante
t
0
=
0
s
até
o
instante
t
=
10
s,
é
uma
reta
crescente,
indicando
um
movimento
uniforme.
Do
instante
t
>
10
s
o
corpo
permanece
em
repouso,
veja
que
a
posição
permanece
a
mesma,
s
=
40
m.
Como
foi
explicado
anteriormente,
a
inclinação
ou declividade da reta nos dará o valor da velocidade.
Veja a resolução na figura ao lado.
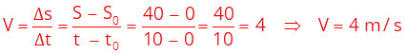
A função horária fica:
s = 2 + 3.t
ciencia-cultura.com
Figura 1
Figura 2
Figura 3
Figura 4
Figura 5
Figura 6


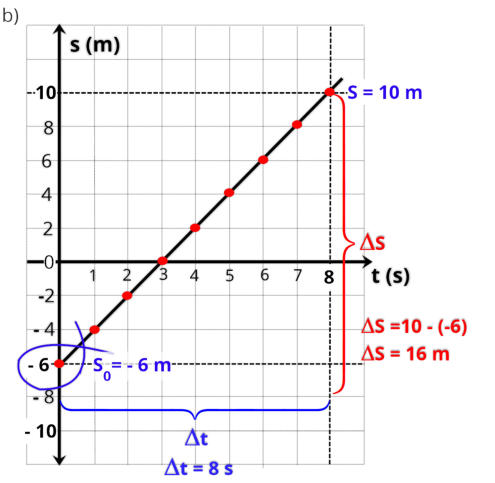
2.3.e Exercícios Resolvidos
R1.
Escreva a equação horária que representa cada um dos gráficos abaixo.
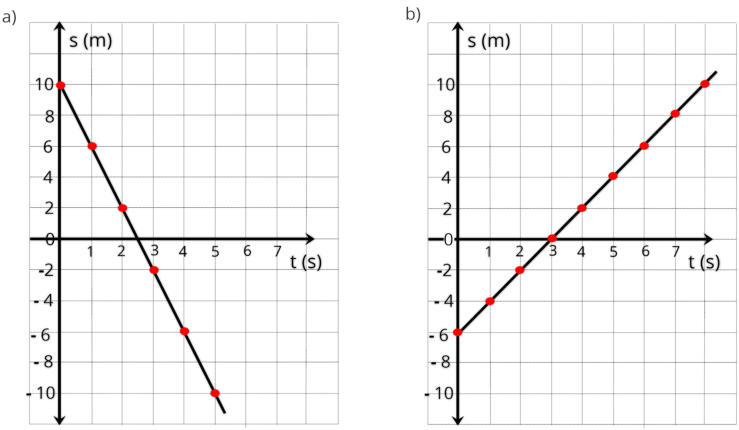
Resolução
Vamos determinar a equação horária,
S= S
0
+ V.t.
O
gráfico
é
uma
reta,
o
que
significa
que
a
função
é
do 1º grau, ou seja, é um movimento uniforme.
Vamos
determinar
a
velocidade
V,
e
a
posição
inicial S
0
.
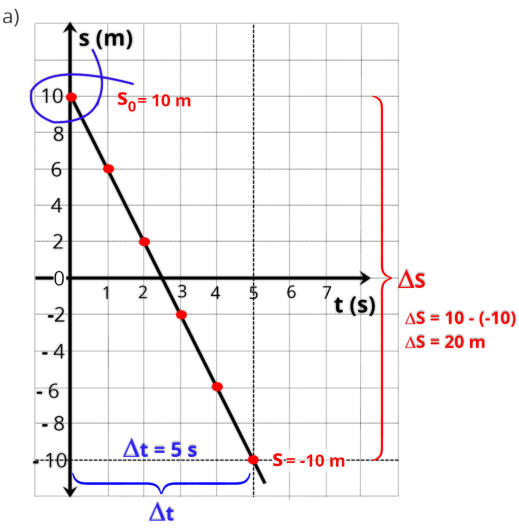
Na
figura
, a reta inicia na
posição inicial S
0
= - 6 m.
Para
a
velocidade
vamos
escolher
dois
pontos
na
reta, a posição inicial (S
0
= -6 m) e a posição final
(S = 10 m) .
A equação é:




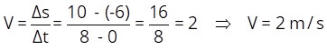

Vamos determinar a equação horária, S= S
0
+ V.t.
O gráfico é uma reta, o que significa que a função
é do 1º grau, ou seja, é um movimento uniforme.
Vamos determinar a velocidade V, e a posição
inicial S
0
.
Na figura, a reta inicia na posição inicial S
0
= 10m.
Para a velocidade vamos escolher dois pontos na
reta, a posição inicial (S
0
= 10 m) e a posição final
(S = - 10 m) .
A equação é:





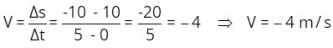
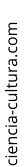
a
)
Resolução:
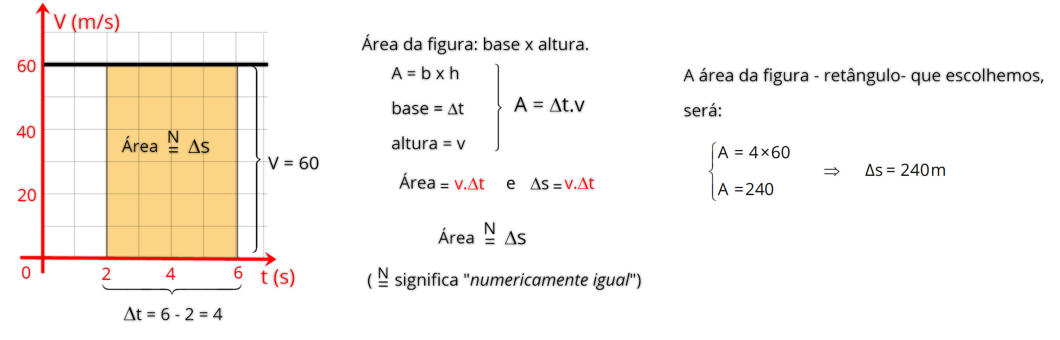
Se considerarmos que um corpo viaja a uma velocidade de 60 m/s, como mostra o gráfico, o espaço percorrido entre os instantes t
1
= 2s e t
2
= 6s
pode ser calculado no gráfico pela propriedade gráfica, veja a resolução a seguir.
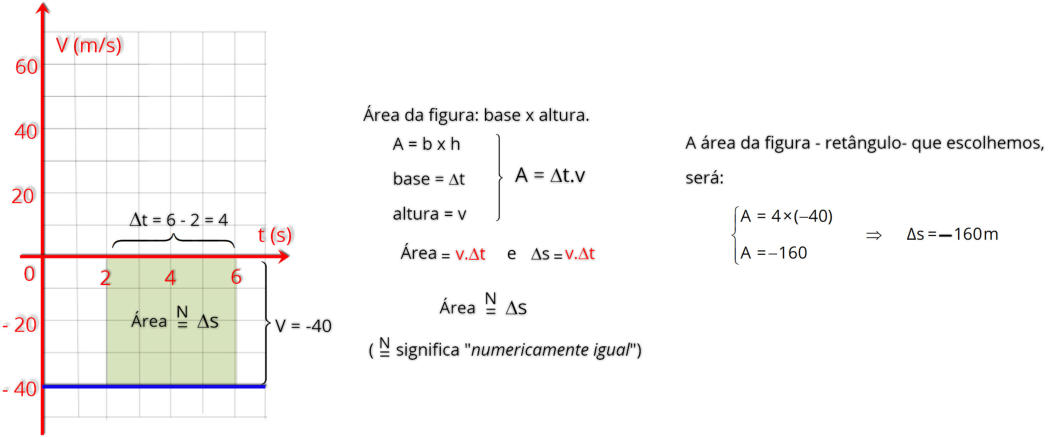
b)
Resolução:
Faremos o mesmo para o corpo que se desloca com uma velocidade de -40 m/s, como mostra o gráfico, o espaço percorrido entre os instantes
t
1
= 2 s e t
2
= 6 s , veja a resolução a seguir.
MRUV - aceleração
Movimento retilíneo uniforme



ciencia-cultura.com





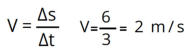

V = 2 m/s













Como colaborar.
Este
site
não
possui
finan-
ciamento algum.
A
forma
que
eu
encontrei
para
arrecadar
fundos,
é
ofertar
a
compra
do
livro
indicado na figura abaixo.
Testes
da
Fuvest
com
reso-
lução comentada.















