Cinemática

Capítulo 3.2 – Movimento circular 3.2.a Introdução

3.2.c Exercícios resolvidos R1. Uma partícula partindo da origem dos espaços, executa um movimento circular, atingindo a posição s = 6 m. Sabendo-se que o raio da circunferência é R = 4 m, determine qual foi o seu deslocamento angular Dj em radianos. Resolução Vamos inicialmente fazer um esquema do movimento da partícula na trajetória circular. R2. Um móvel se desloca sobre uma trajetória circular cujo raio mede R = 4 m. No instante inicial sua posição é s 0 = 4 m, e no instante t ocupa a posição s = 12 m. Determine o deslocamento angular do móvel neste intervalo de tempo. Resolução Vamos inicialmente fazer um esquema do movimento da partícula na trajetória circular. R3. Determine em radianos os seguintes arcos: da circunferência, circunferência e da circunferência. Resolução: Lembrando que o comprimento de uma volta na circunferência é: 3.2.d Deslocamento linear e deslocamento angular Uma partícula ao descrever um movimento circular pode ser descrita de duas maneiras; utilizando grandezas lineares ou grandezas angulares . Uma partícula ao se deslocar sobre uma trajetória curvilínea, parte da posição inicial s 0 , decorrido certo intervalo de tempo D t ela se encontra na posição s . Pelo fato da nossa trajetória ser curvilínea podemos descrever esta mesma situação de outra forma, uma partícula partiu no instante t 0 de uma posição angular j 0 , e decorrido certo intervalo de tempo D t, ela se encontra na posição j . Desta forma a partícula sofreu um deslocamento angular Dj em um intervalo de tempo D t . 3.2.e Velocidade escalar média e velocidade média angular. Podemos estabelecer uma relação entre a velocidade média escalar V M com a velocidade média angular w M . Vimos anteriormente que a velocidade escalar média de um corpo, corresponde ao espaço percorrido num certo intervalo de tempo. 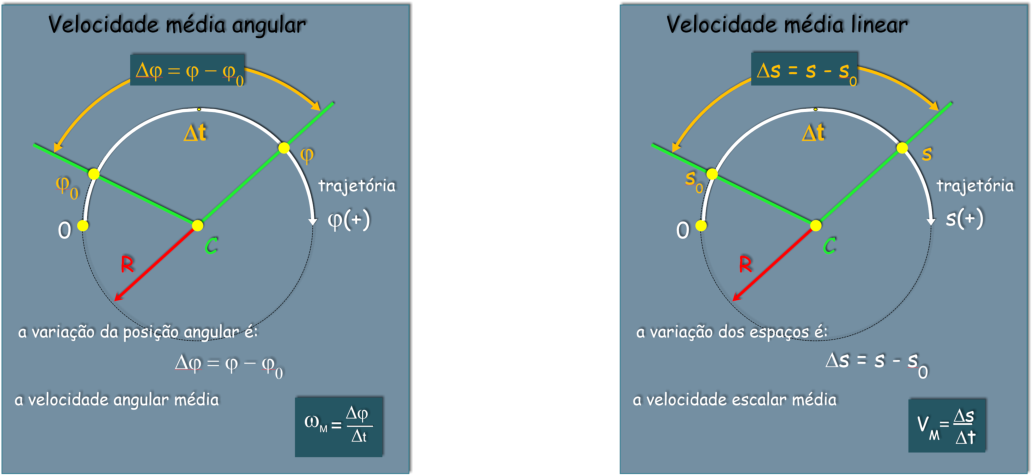Da mesma forma, podemos definir a velocidade média angular w M , como sendo um deslocamento angular Dj em um intervalo de tempo D t, como mostramos na figura abaixo.

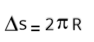
Podemos estabelecer uma relação entre o período T e a freqüência de um movimento por uma simples regra de três: Agora podemos estabelecer uma relação entre a velocidade angular média com a frequência e período para um movimento circular uniforme. 3.2.f Exercícios resolvidos R4. Dada uma circunferência cujo raio R = 3 m, um ângulo central cujo arco mede s = 12 m. Determine o valor do ângulo central em radianos. Resolução: Vamos inicialmente construir uma figura para ilustrar o que o problema nos diz. R5. Um ponto material descreve um movimento circular. No instante t = 2 s o seu espaço é s 0 = 3 m, e o instante t= 5 s e o seu espaço s = 9 m. O raio da circunferência é R = 4 m. Determine: a) o deslocamento angular do ponto material no intervalo de 2 s a 5 s; b) a velocidade angular média no mesmo intervalo de tempo. Resolução: Vamos inicialmente construir uma figura para ilustrar o que o problema nos diz. R6. Uma roda gira com freqüência 1200 rpm. Deterrmine freqüência e o período desta roda no sistema internacional SI. 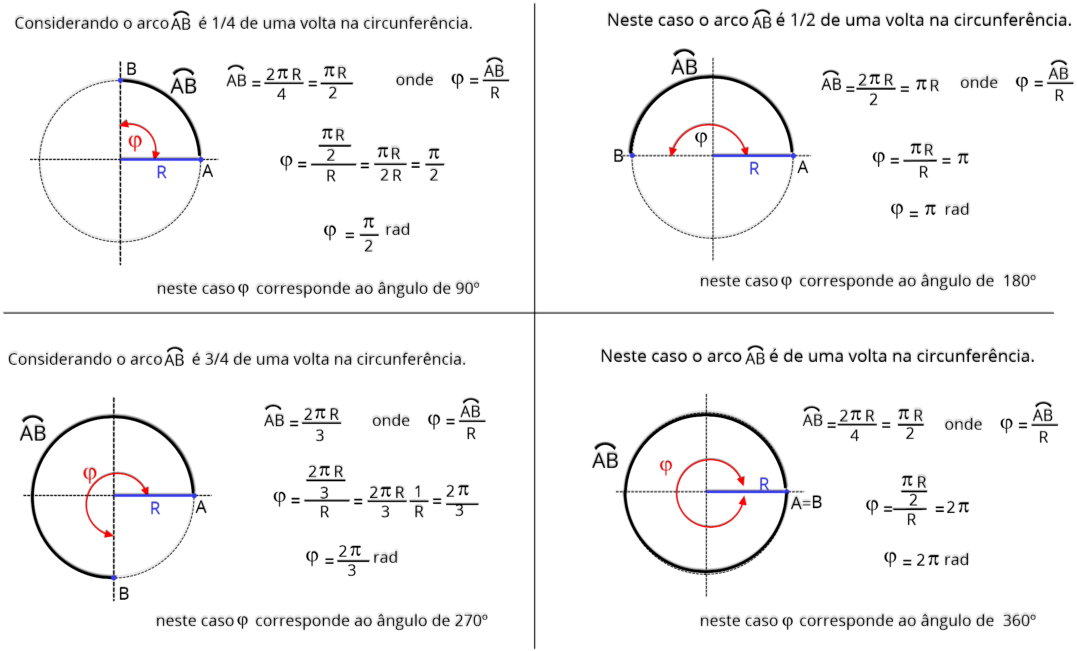Resolução: No sistema internacional a frequência é medida em Hz (hertz) e o período em s (segundos). Assim devemos transformar a unidade rotações por minuto (rpm) em rotações por segundo que equivale a hertz.

3.2.h Exercícios propostos P1 O espaço percorrido por um móvel, que realiza movimento circular uniforme de raio R = 0,1 m, é num certo instante, s = 0,8 m. Determine qual deve ser o deslocamento angular do móvel. P2. A velocidade escalar de um móvel ao realizar um movimento circular uniforme de raio R = 0,2 m é v = 5 m/s. Determine a velocidade angular do móvel. P3. Uma partícula realiza um movimento circular uniforme, completando 5 voltas em 20 s. Determine: a) a sua frequência; b) o período da partícula. P4. O deslocamento angular de um corpo, ao realizar um movimento circular uniforme de raio R = 10 cm, corresponde a D j = p/2 rad. Determine o correspondente deslocamento escalar pare este corpo. P5. Um corpo realiza um movimento circular uniforme com velocidade angular w = 10 rad/s. Sendo o raio da trajetória R = 0,3 m, determine sua velocidade escalar. P6. (Uerj) Uma pequena pedra amarrada a uma das extremidades de um fio inextensível de 1 m de comprimento, preso a um galho de árvore pela outra extremidade, oscila sob ação do vento entre dois pontos equidistantes e próximos à vertical. Durante 10 s, observou-se que a pedra foi de um extremo ao outro, retornando ao ponto de partida, 20 vezes. Calcule a frequência de oscilação desse pêndulo. P7. Uma barra de comprimento L = 5 m gira em torno de um ponto fixo O. Os pontos da barra descrevem movimentos circulares e uniformes. O ponto A, situado na extremidade da barra, realiza um deslocamento angular w = 2 rad num intervalo de tempo Dt = 4 s. Determine: a) a velocidade angular do ponto A; b) a velocidade escalar do ponto A.

Trataremos agora do movimento de um corpo que percorra uma trajetória circular. Utilizando os conceitos que vimos na cinemática, poderemos falar em espaço percorrido (  s), intervalo de tempo (  t), velocidade escalar média, e se o módulo da velocidade for constante teremos o movimento circular uniforme. Mais adiante, utilizaremos as leis de Newton para saber o comportamento das forças durante o movimento circular, como um trem na montanha russa, um carro fazendo uma curva, um satélite orbitando um planeta, a roda gigante e muitas outras situações, que denominamos dinâmica do circular. 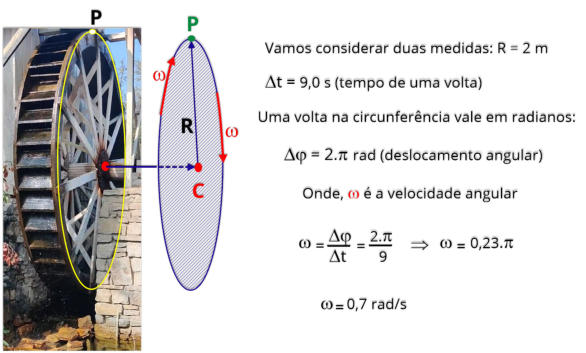No vídeo ao lado mostramos uma roda d’água, como o nome diz a queda da água possibilita a execução de um movimento circular, e se considerarmos que o módulo da velocidade é constante, denominaremos movimento circular uniforme. Vamos utilizar a cinemática e com boa aproximação vamos determinar a velocidade escalar média de um ponto P na sua extremidade como mostra a figura abaixo. 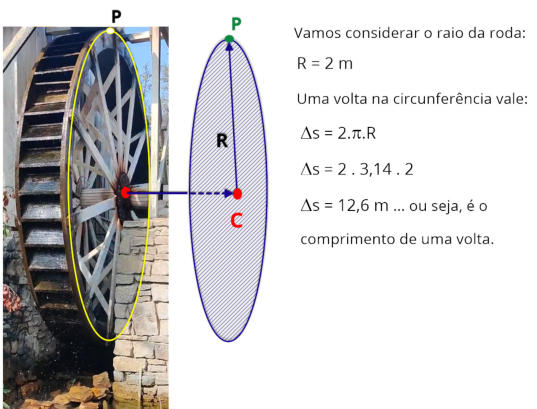Considerando que a roda d’água possua um raio de 2,0 m, podemos determinar a distância que o ponto P percorrerá para dar uma volta, veja a resolução a seguir.

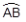
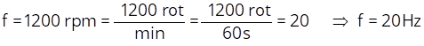
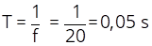
Podemos estabelecer uma relação entre a velocidade média escalar V M com a velocidade média angular w M . Veja como isto pode ser feito:

Agora que definimos as grandezas angulares, podemos retornar ao exemplo da roda d’água analizando o movimento através de grandezas angulares.

3.2.b Introdução as grandezas angulares O movimento circular do exemplo acima, também pode ser estudado utilizando grandezas angulares, já que a nossa trajetória será sempre uma circunferência. Quando estudamos ângulos na geometria, é comum utilizarmos a unidade “graus”, no entanto no Sistema Internacional (SI) a medida do ângulo é dada em radianos. O radiano, ou pelo símbolo rad, é utilizado na matemática e física. 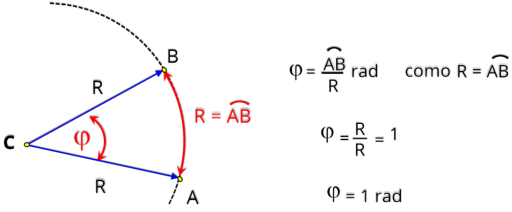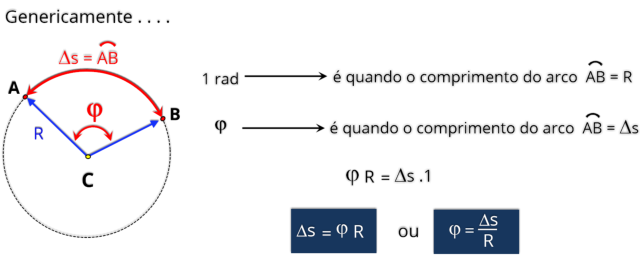Na figura abaixo, mostramos que o radiano ( j = 1 rad ) é o ângulo definido em um círculo por um arco de circunferência , com o mesmo comprimento que o raio do referido círculo.

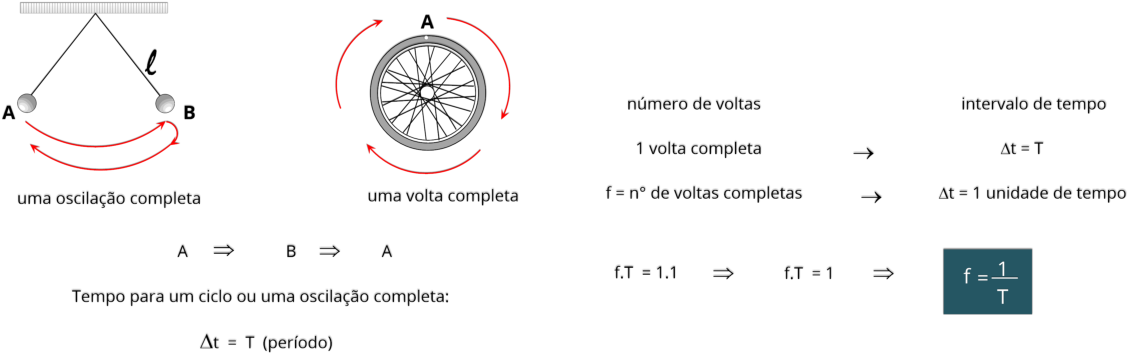
Um arco de circunferência cujo comprimento é igual ao raio r (em vermelho) corresponde a um ângulo de 1 radiano (em verde). A metade da circunferência corresponde a π radianos e uma circunferência completa a 2π. Wikipedia

FONTE DE LUZ SÍNCROTRON SIRIUS Sirius, a nova fonte de radiação síncrotron brasileira, funciona como um grande microscópio que − ao revelar a estrutura atômica, molecular e eletrônica dos mais diversos materiais – permite pesquisas com aplicações em praticamente todas as áreas do conhecimento. Para produzir a radiação síncrotron, feixes de elétrons são acelerados em várias etapas até alcançarem o anel principal do acelerador Sirius, um tubo fechado onde se produz vácuo. Nesse espaço confinado, os elétrons se movimentam em trajetória circular com rapidez próxima à da luz. Adaptado de lnls.cnpem.br. P8. (Uerj 2024) Admita que os feixes de elétrons, ao percorrerem o anel principal do Sirius, completam, com rapidez constante, 80.000 voltas em um segundo. Admita, ainda, que o raio do anel possui 500 m e π = 3. Calcule, em segundos, o período do movimento circular dos elétrons e determine, em m/s, a rapidez alcançada por esses elétrons no acelerador Sirius.

P9. (Unifesp 2017) Um avião, logo após a aterrissagem, está em movimento retilíneo sobre a pista horizontal, com sua hélice girando com uma frequência constante de 4 Hz Considere que em um determinado intervalo de tempo a velocidade escalar desse avião em relação ao solo é constante e igual a 2 m/s que cada pá da hélice tem 1 m de comprimento e que π = 3. Calcule a distância, em metros, percorrida pelo avião enquanto sua hélice dá 12 voltas completas.

P10. (Uerj 2012) Uma pequena pedra amarrada a uma das extremidades de um fio inextensível de 1 m de comprimento, preso a um galho de árvore pela outra extremidade, oscila sob ação do vento entre dois pontos equidistantes e próximos à vertical. Durante 10 s, observou-se que a pedra foi de um extremo ao outro, retornando ao ponto de partida, 20 vezes. Calcule a frequência de oscilação desse pêndulo.

Vamos considerar que a roda de uma volta em um intervalo de tempo de aproximadamen- te Dt = 9,0 s.

Com os valores do espaço percorrido e do tempo, determinamos o módulo da velocidade de rotação da roda d’água, como mostramos a seguir.

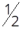
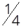
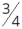
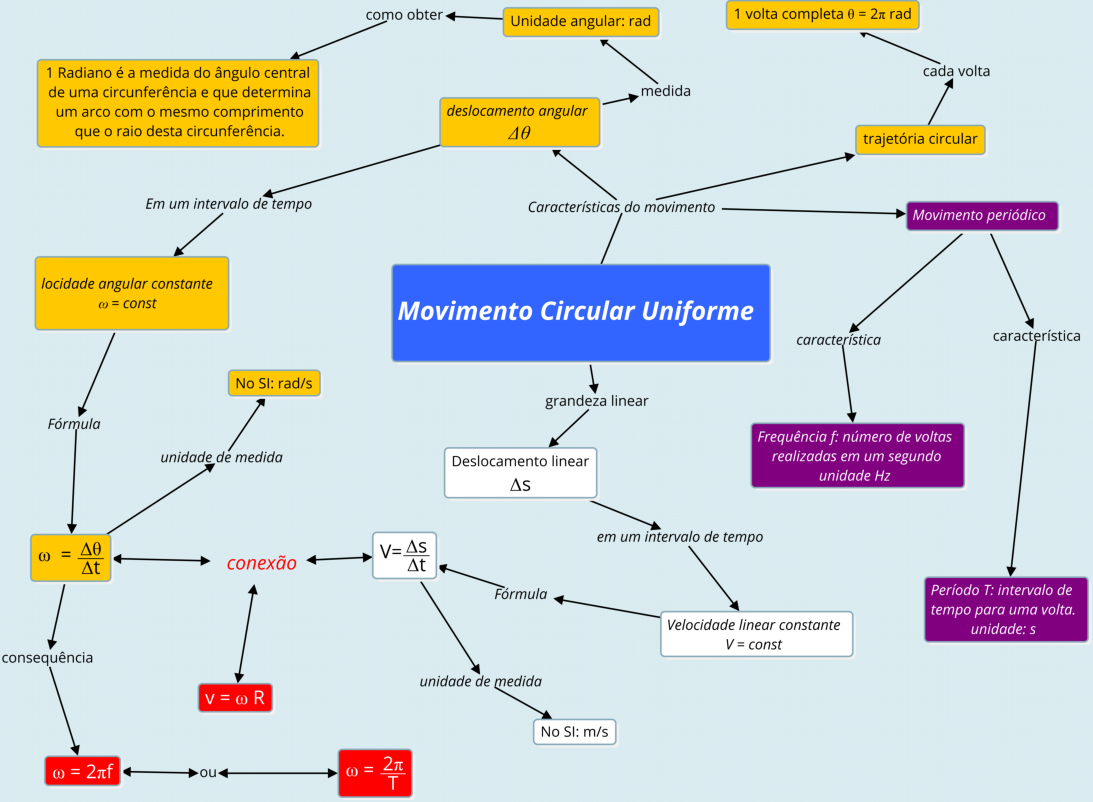
3.2.g Mapa conceitual

Procure fazer o teu mapa conceitual, vai te ajudar a organizar os conceitos desta lição.

A característica do movimento circular uniforme é o de manter a velocidade angular constante. Isto significa que a partícula ao percorrer uma trajetória circular apresenta todas as características de um movimento uniforme acrescentando as particularidades desta forma de trajetória. Uma característica importante do movimento circular uniforme é a sua periodicidade, ou seja, a partícula ao dar uma volta completa, repetirá este movimento em intervalos de tempo sempre iguais. A este intervalo de tempo sempre constante, que corresponde à duração do tempo para completar uma volta, damos o nome de período T . Outra grandeza importante no MCU é a freqüência do movimento. A freqüência f mede o número de voltas que a partícula realiza por unidade de tempo . Suas unidades usuais são: