
2.8.b
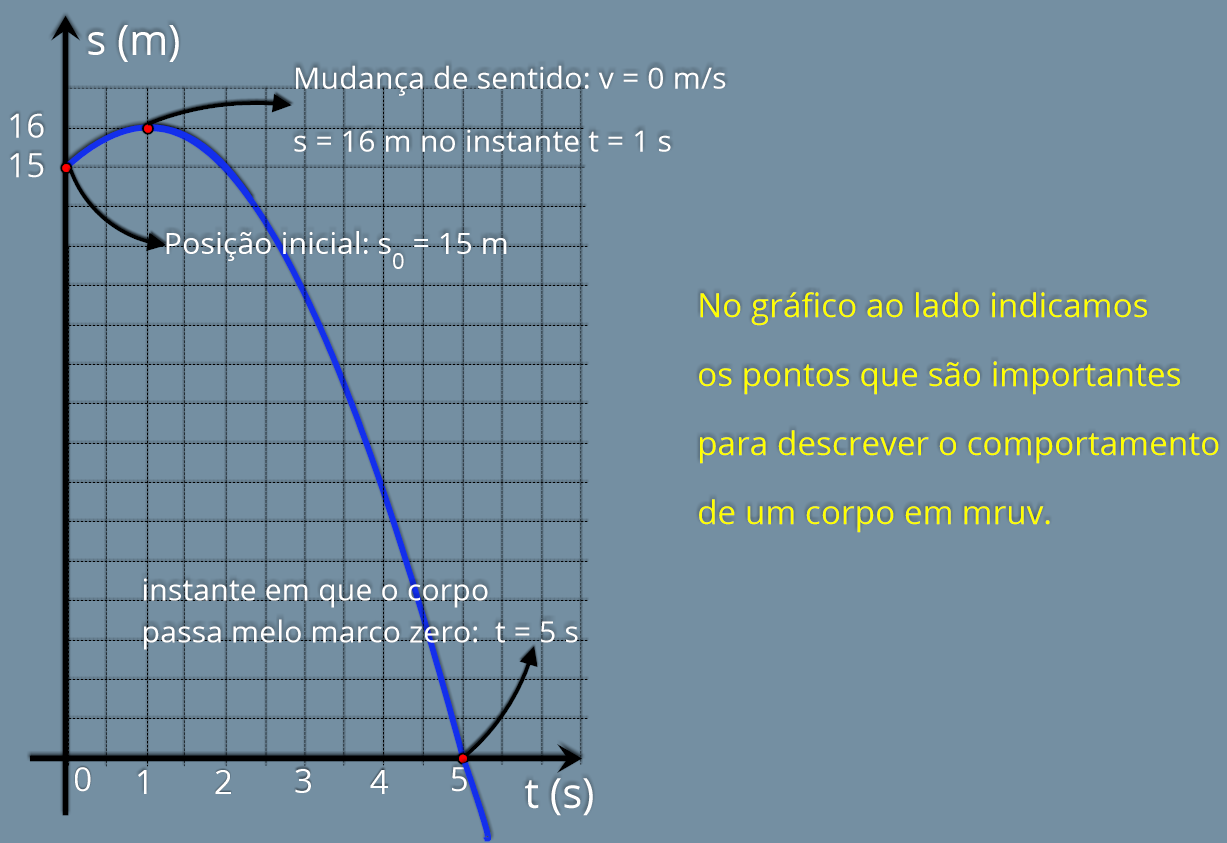
Gráfico posição x tempo - s = f (t)
Nada
como
mostrar
alguns
exempos
para
termos
uma
idéia
“concreta”
sobre
aquilo
que
acabamos
de
ler.
Inicialmente
vamos
examinar
no
movimento
retilíneo
uniformemente
variado,
o
gráfico
da
posição
(s)
em
função
do
tempo
(t).
Relembrando,
a
equação
horária
de
posição
é
uma
equação do 2º grau.
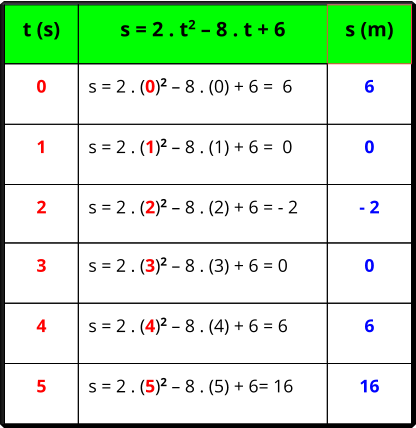
Como exemplo vamos utilizar uma equação para entender o que um gráfico pode nos fornece de informações sobre o movimento.
S = 6 - 8.t + 2.t
2
Vamos
inicialmente
construir
um
gráfico
com
a
equação
fornecida,
montamos
uma
tabela
e
vamos
atribuir
valores
para
o
tempo,
procurando
sempre
escolher
números
que
não
criem
dificuldade
no
cálculo.
Feito
isto,
obteremos
os
valores
para
a
posição
(s)
em
função
do
tempo (t), como mostramos na tabela abaixo.


© COPYRIGHT 2000 - CIENCIA-CULTURA.COM - TODOS OS DIREITOS RESERVADOS - Responsável - Ricardo Pante
Índice das aulas de física

Cinemática

2.8 Gráficos do movimento retilíneo uniformemente variado
2.8.a
Introdução -
Para que serve um gráfico na cinemática?
Quais seriam as informações importantes no gráfico sobre o movimento?
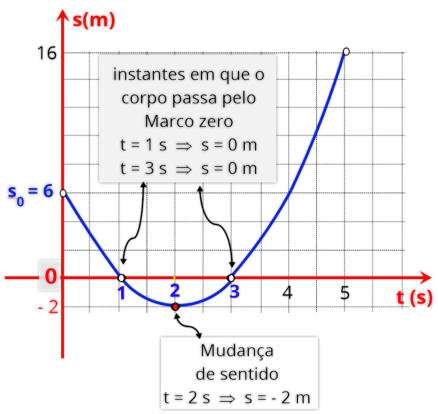
Na
imagem
do
gráfico
ao
lado,
podemos
conferir
algumas
informações
sobre o movimento:
A
posição
inicial
do
movimento,
S
0
=
6
m
,
local
onde
começa
o
gráfico
no
eixo de posição (s);
O
corpo
passa
pelo
marco
zero
(
s
=
0
m)
em
dois
momentos,
no
instante
t
=
1
s
e
em
t
=
3
s,
isso
se
deve
ao
fato
que
nestes
dois
instantes
o
eixo
da
posição indica
s = 0 m
;
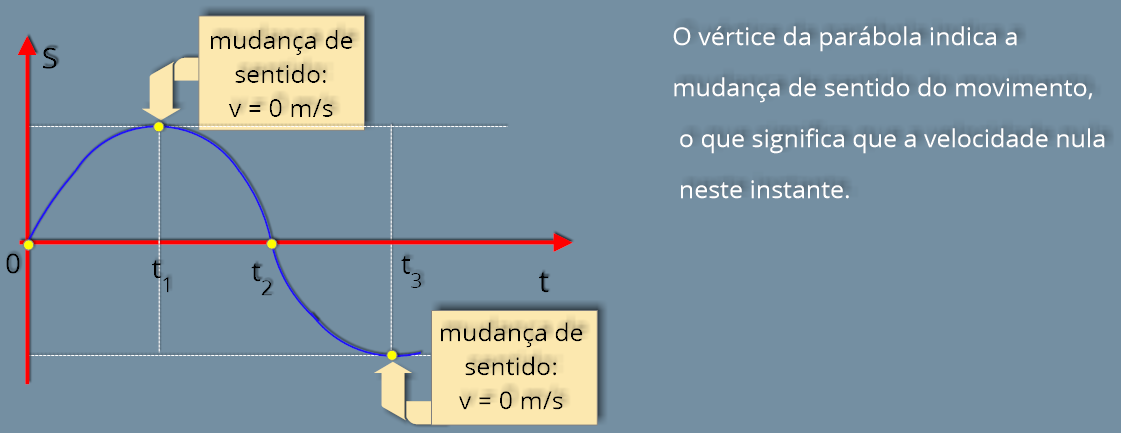
O corpo muda o sentido do movimento, na posição
s = - 2 m
, no instante
t
=
2
s.
Local
que
indica
que
a
velocidade
é
nula.
Inicialmente
o
movimento
é
contra
a
trajetória,
até
chegar
na
posição
s
=
-2
m
,
a
partir
desta
posição,
o
seu movimento concorda com o sentido da trajetória.
2.8.c
Exercícios Resolvidos
R1.
Um
corpo
executa
um
movimento
retilíneo
uniformemente
variado
cuja
posição
s,
é
medida
na
trajetória
em
metros,
a
partir
de
uma
origem,
e
o
tempo
(t)
em
segundos,
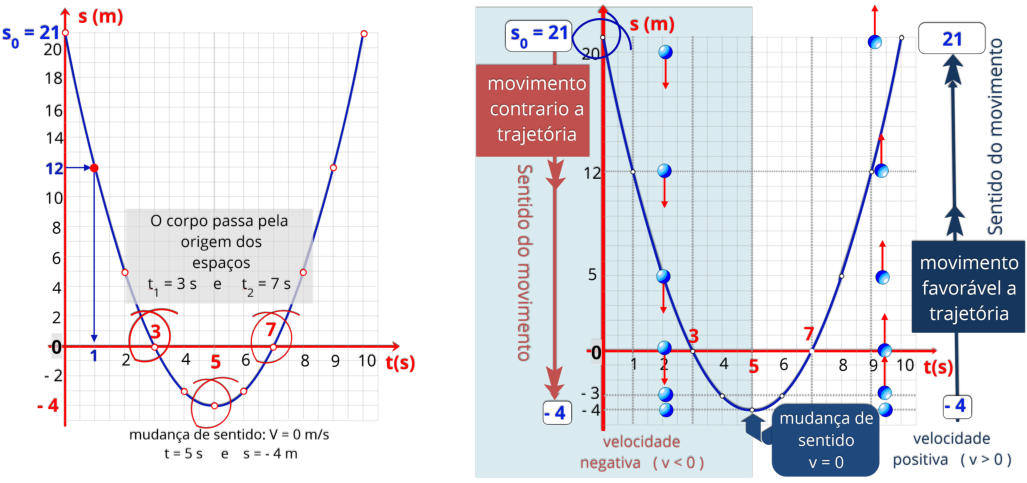
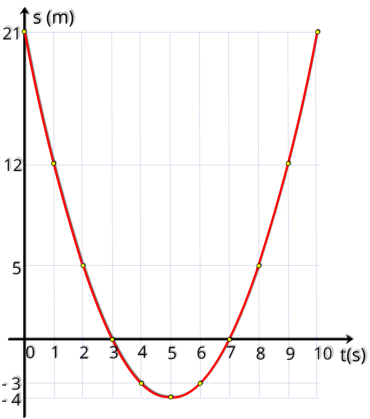
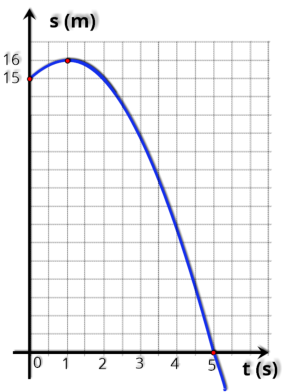
conforme mostramos no gráfico. Assinale no gráfico:
a) a posição inicial do corpo,
b) o instante e a posição em que o corpo muda de sentido,
c) o instante em que o corpo passa pela origem dos espaços.
Resolução:
Vamos indicar no gráfico os pontos que nos sãos solicitados no exercício. Veja a figura abaixo
a) a posição inicial do corpo :
S
0
= - 21 m
b) o instante e a posição em que o corpo muda de sentido:
t = 5 s e S = - 4 m
c) o instante em que o corpo passa pela origem dos espaços:
t
1
= 3 s e t
2
= 7 s
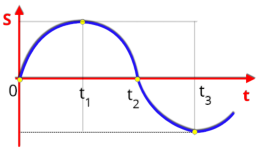
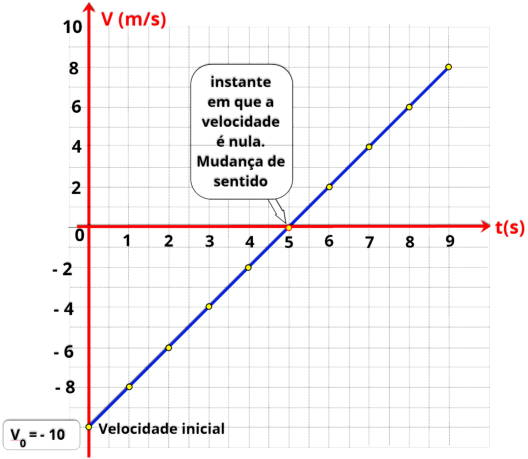
P2.
Analise
o
gráfico
de
posição
em
função
do
tempo,
e
mostre
em
que
instantes
a
velocidade
é nula.
2.8.d
Exercícios propostos
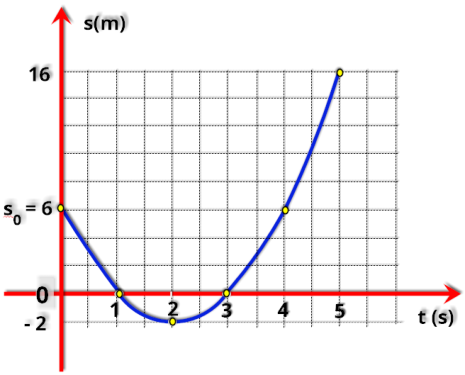
P1.
Analise
o
gráfico
ao
lado,
o
qual
representa
o
movimento
de
um
corpo,
que
executa
um
movimento
retilíneo
uniformemente
variado.
As
grandezas
posição
(s)
e
tempo
(t)
são
medidos
na
trajetória
em
metros
e
segundos
respectivamente,
a
partir
de
uma
origem.
Encontre no gráfico:
a) a posição inicial do corpo,
b) o instante e a posição em que o corpo muda de sentido,
c) o instante em que o corpo passa pela origem dos espaços.
2.8.e
Gráfico da velocidade x tempo - V = f (t)
Da
mesma
forma
que
fizemos
com
o
gráfico
da
posição
em
função
do
tempo,
faremos
o
mesmo
com
o
gráfico
da
velocidade
em
função
do tempo. Três informações podem ser obtidas pela análise do gráfico de v x t, que são elas:
Determinação da aceleração do movimento;
Determinação da variação dos espaços;
Determinação da velocidade inicial

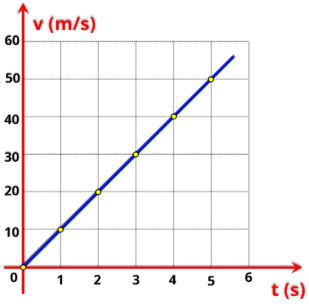
Com os dados da tabela, podemos construir o gráfico V x t. A função horária da velocidade no MRUV é do 1º grau, motivo pelo qual
obtivemos uma reta. Veja o gráfico acima.
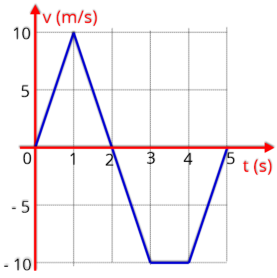
Indicamos no gráfico dois pontos importantes: o início da reta, ou seja, a velocidade inicial
V
0
= - 10 m/s,
e em
t = 5 s
a velocidade é nula
(V
=
0
m/s),
indicando
que
o
movimento
muda
o
seu
sentido.
É
importante
lembrarmos
que
no
instante
em
que
a
velocidade
é
nula
no
MRUV,
significa que ocorre uma mudança no sentido do movimento.
Como
exemplo,
vamos
construir
o
gráfico
da
velocidade
em
função
do
tempo para a função
v = - 10 + 2t,
em unidades do SI.
Facilita
e
organiza
nosso
cálculo
se
construirmos
uma
tabela,
onde
daremos
valores
para
o
tempo,
e
obteremos
valores
para
a
velocidade,
como
mostramos na tabela a seguir.
Vamos
determinar
a
aceleração
do
movimento
analisando
o
gráfico
que
acabamos
de
construir.
A
forma
como
a
reta
é
inclinada,
nos
informa
sobre
o
valor
da
aceleração,
ou
seja,
a
declividade
da
reta
representada
pelo
ângulo
q
.
Escolhendo
o
V
0
=
-10
m/s
e
a
velocidade
final
(ponto
A)
V
=
8
m/s,
podemos
obter
o
valor
de
D
V
e
D
t
,
onde
a
razão entre o lado
D
V por
D
t , é:
resolvendo teremos:
A
conclusão
a
que
chegamos
com
este
exemplo,
é
a
de
que
a
aceleração
é
constante
e
seu
valor
será
a
=
2
m/s
2
.
Com
este
valor
e
o
valor
de
V
0
=
-10
m/s,
podemos
escrever
a
função
horária
da
velocidade como:
V = - 10 + 2 t
2.8.f Determinação da aceleração do movimento
2.8.g Exercícios Resolvidos
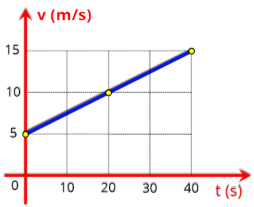
R2. Determine em cada um dos casos apresentados a seguir, a respectiva equação horária da velocidade.
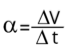
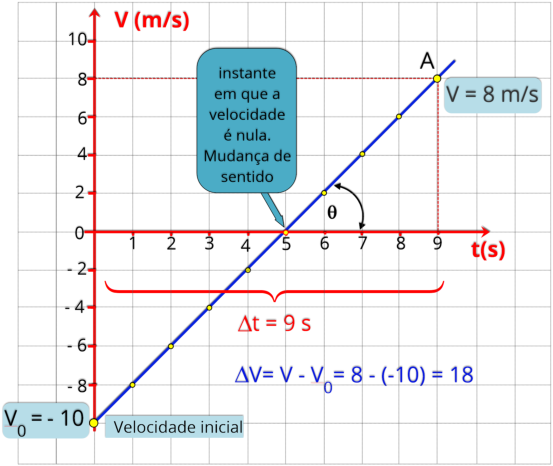
a) Resolução
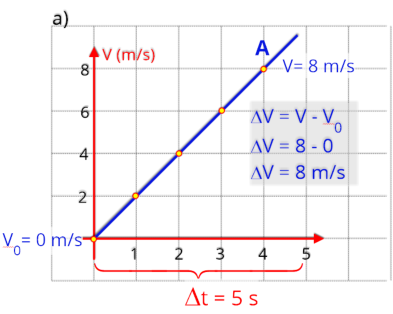
Inicialmente
devemos
determinar
a
velocidade
inicial
e
a
aceleração,
com
estes
dois
valores
podemos
escrever
a
função
horária.
A
velocidade
inicial
é
indicada
no
gráfico, por onde tem início a reta, neste caso
V
0
= 0 m/s
.
A
variação
da
velocidade
é
de
V
0
=
0
m/s
até
V
=
8
m/s
(ponto
A),
levando
5
segundos para que isto ocorra, veja no gráfico.
Sendo a equação:
V = V
0
+
a
t,
teremos:
V = 0 + 1,6.t,
simplificando:
V= 1,6 t (SI)
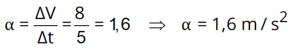
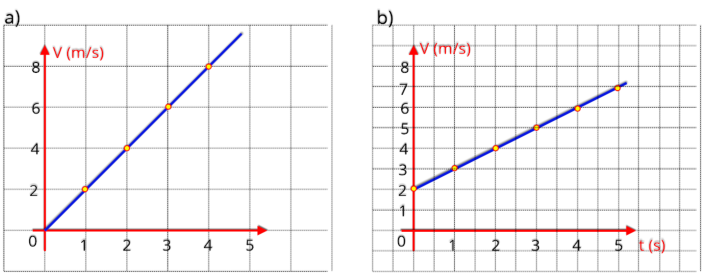
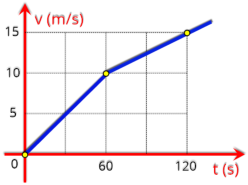
b) Resolução
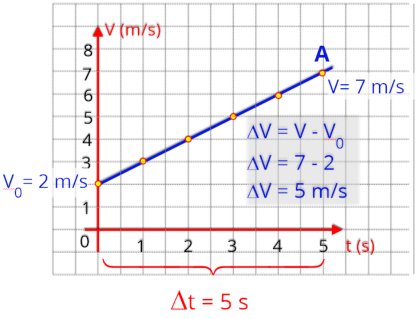
Vamos
determinar
a
velocidade
inicial
e
a
aceleração,
com
estes
dois
valores
podemos
escrever
a
função
horária.
A
velocidade
inicial
é
indicada
no
gráfico,
por
onde tem início a reta, neste caso
V
0
= 2 m/s.
A variação da velocidade é de
V
0
= 2 m/s
até
V = 7 m/s
(ponto A), levando
5 segundos para que isto ocorra, veja no gráfico.
Sendo a equação:
V = V
0
+
a
t
, teremos:
V = 2 + 1.t, (SI)
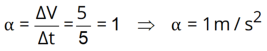
2.8.h
Exercícios propostos
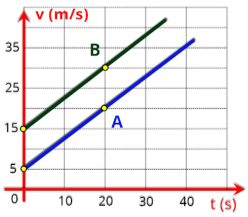
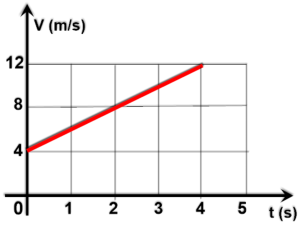
P3.
O
gráfico
ao
lado
representa
a
variação
da
velocidade
de
um
corpo
em
função
do
tempo.
Determine
a função horária da velocidade que descreve este movimento.
P4.
Um
carro,
partindo
do
repouso,
percorre
dois
trechos
de
uma
rodovia
com
uma
velocidade
variável
conforme está representado no gráfico ao lado.
a) Qual a aceleração do carro no primeiro trecho do percurso?
b) Qual é a aceleração do carro durante o segundo trecho do percurso?
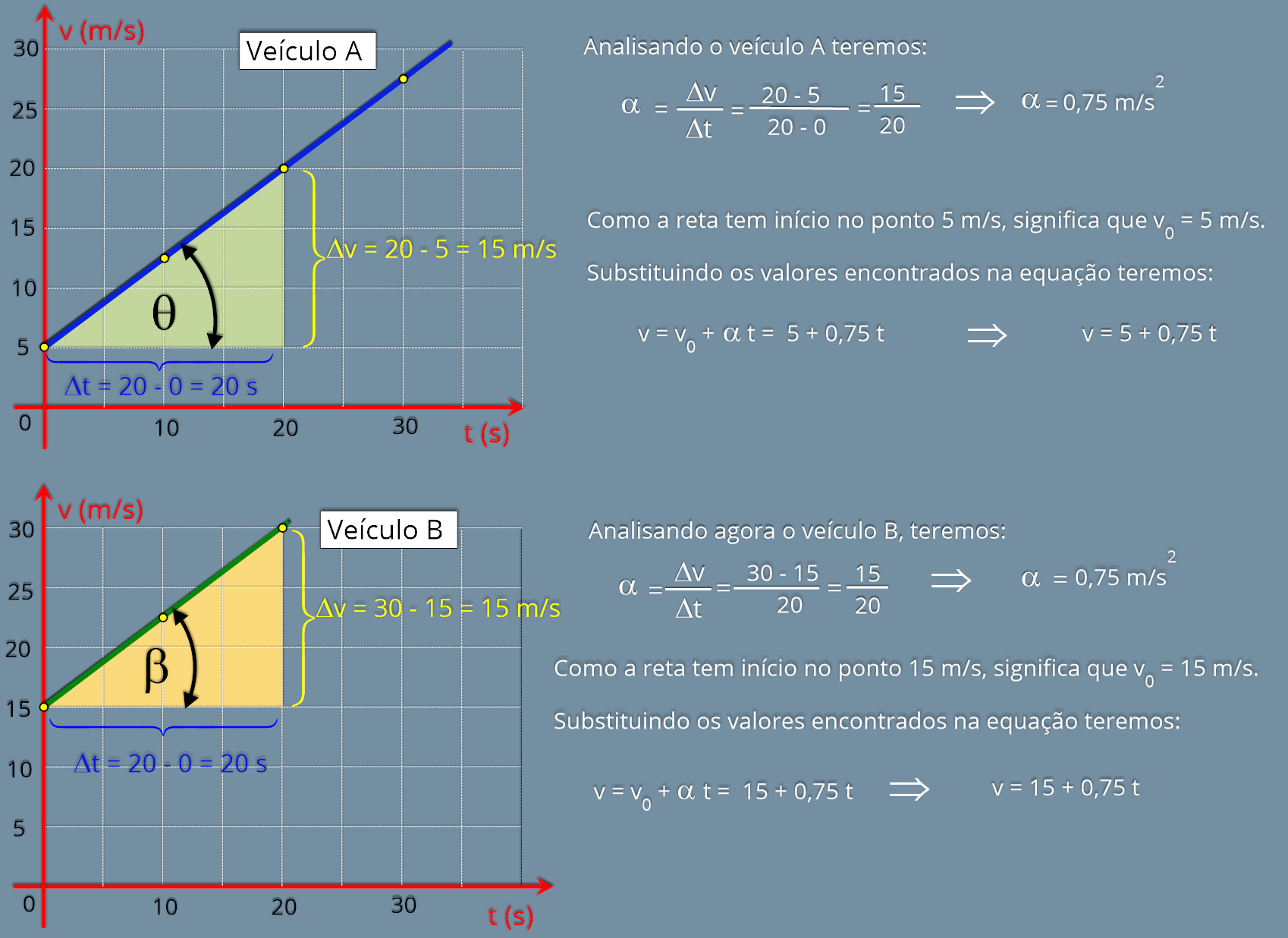
P5.
Dois
veículos
A
e
B,
movimentando-se
em
uma
mesma
rodovia,
onde
seus
movimentos
são
descritos
pelo
gráfico
ao
lado.
Determine
em
cada
caso
a
função
horária
da
velocidade
e,
verifique
o
que
existe
em comum com estes dois movimentos.
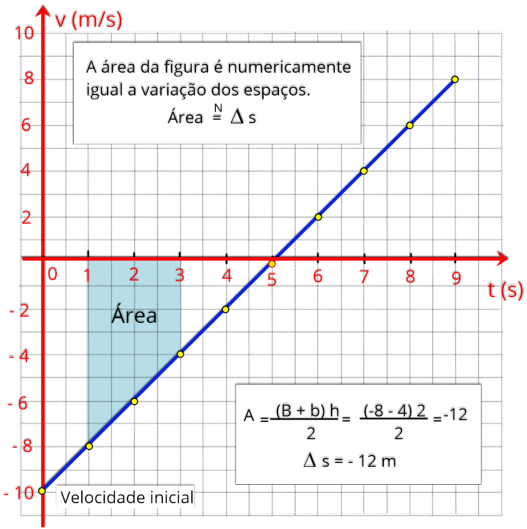
A
segunda
propriedade,
relaciona
a
área
de
um
gráfico
da
velocidade
pelo
tempo
à
variação
dos
espaços
(
D
s),
esta
propriedade
foi
estudada
no
movimento
retilíneo
uniforme.
Da
mesma
forma
que
ocorreu
no
MRU,
ocorrerá
no
movimento
retilíneo
uniformemente
variado.
Vejamos
no
gráfico
a
seguir
qual
é
a
variação
de
posição
que
ocorre
entre
os instantes
t = 1 s e t = 3 s
.
Concluímos
neste
exemplo
que
o
deslocamento
sofrido
pelo corpo entre os instantes
t = 1 s a t = 3 s,
de
D
s = - 12 m
.
2.8.j Exercícios Resolvidos
R2.
O
movimento
de
um
corpo
é
representado
pelo
gráfico
da
velocidade
em
função
do
tempo.
Determine:
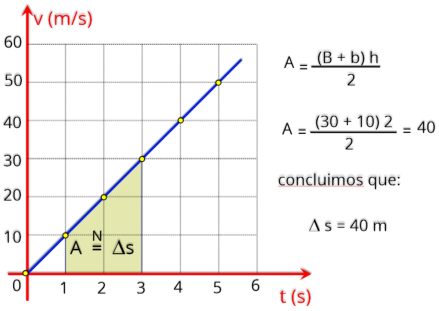
a) o deslocamento do corpo entre os instantes t = 1 s e t = 3 s.
Resolução:
Ao
unirmos
os
pontos
t
=
1
s
e
t
=
3
s
com
a
reta
do
gráfico,
encontraremos
uma
figura
conhecida
como
trapézio.
Veja
a
figura.
O
valor
numérico
que
encontrarmos
para
a
área
do
trapézio,
corresponde ao deslocamento sofrido pelo corpo.
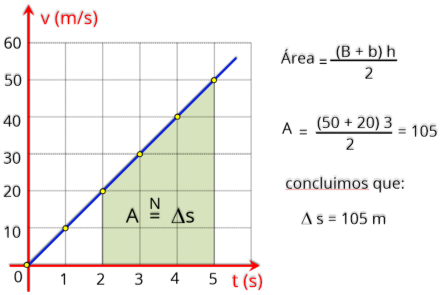
b) o deslocamento do corpo entre os instantes t = 2 s e t = 5 s.
Resolução:
Da
mesma
forma
que
fizemos
no
item
anterior,
partindo
dos
instantes
t
=
2
s
até
t
=
5
s,
formamos
uma figura conhecida como trapézio. Verifique na figura.
O
valor
numérico
da
área
desta
figura
corresponde
ao
valor
do
deslocamento
sofrido
pelo
corpo
entre os instantes t = 2 s e t = 5 s.
2.8.l Exercícios propostos
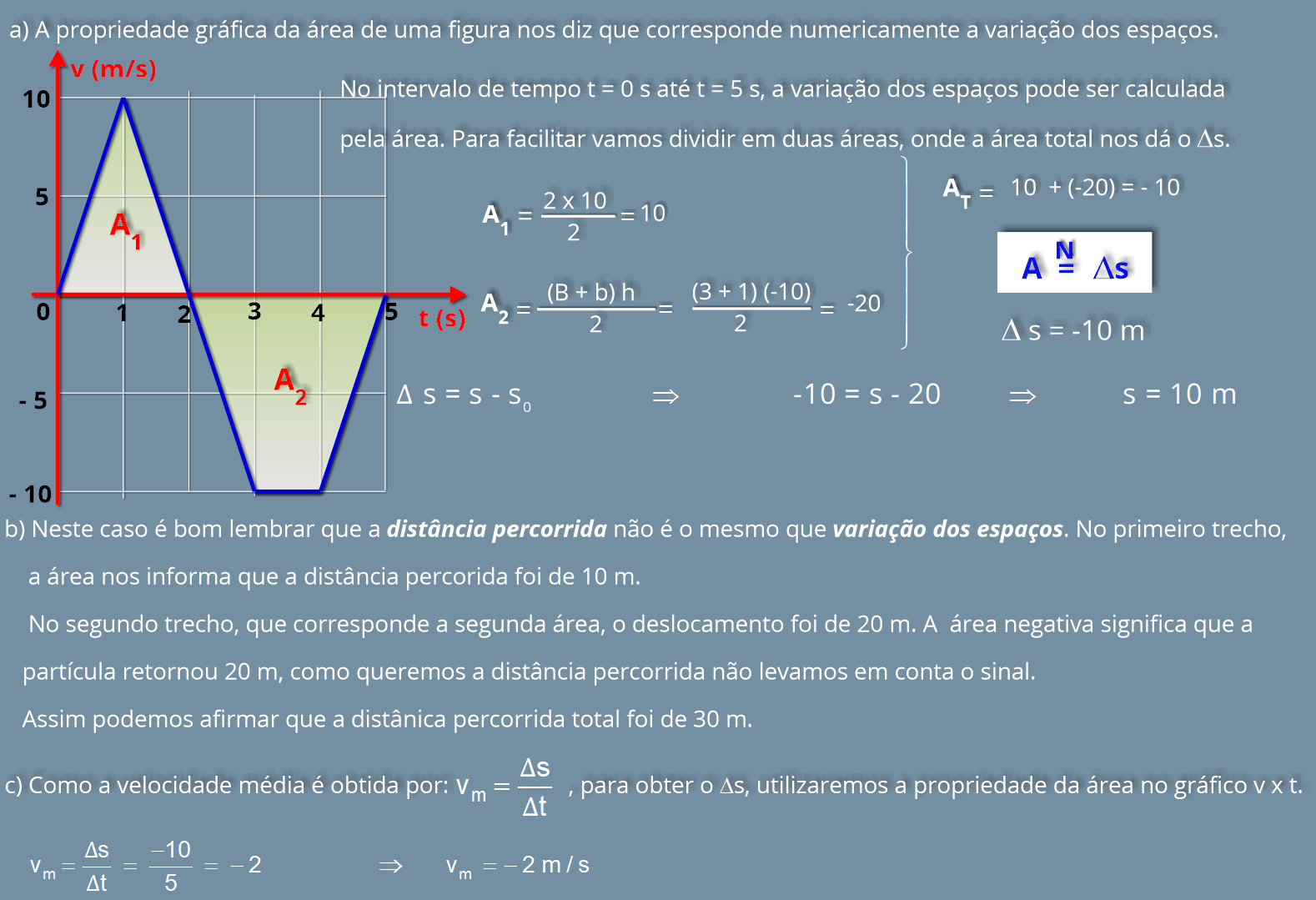
P6.
(UERJ
2009)
A
velocidade
de
um
corpo
que
se
desloca
ao
longo
de
uma
reta,
em
função
do
tempo,
é
representada pelo gráfico. Calcule a velocidade média desse corpo no intervalo entre 0 e 30 segundos.
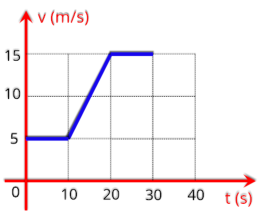
P7.
(Inatel)
Na
figura
vemos
o
gráfico
da
velocidade
de
uma
partícula
em
função
do
tempo.
O
movimento
da partícula começou quando ela estava na posição s
o
= 20 m.
Calcule:
a) a posição da partícula no instante t = 5 s;
b) a distância percorrida pela partícula entre t = 0 e t = 5 s;
c) a velocidade média desenvolvida pela partícula entre t = 0 e t = 5 s.
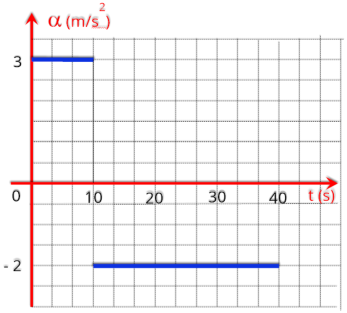
2.8.m
Gráfico da aceleração x tempo -
a
= f (t)
No
movimento
uniformemente
variado,
aprendemos
que
a
velocidade
sofre
variação,
porém
de
maneira
uniforme.
O
significado
físico
da
variação
da
velocidade
no
tempo
conhecemos
como
aceleração.
Pelo
fato
da
aceleração
ser
constante
e
diferente
de
zero,
teremos
sempre
uma
reta
paralela
ao
eixo
do
tempo
como
pode
ser
visto
a
seguir,
onde
neste
caso
sua
aceleração
é
-
4
m/s
2
.
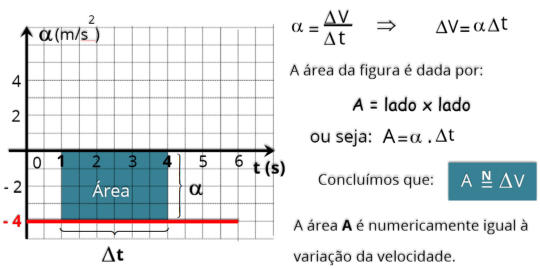
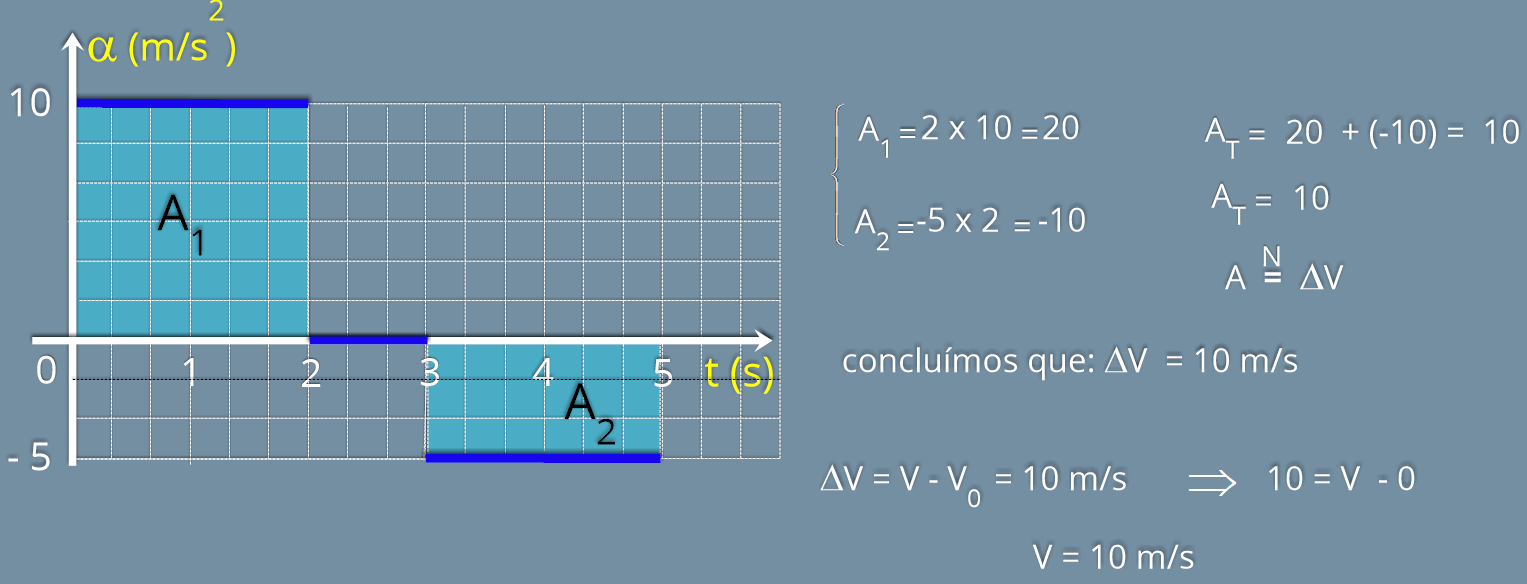
No
gráfico
da
aceleração
podemos
determinar
através
da
área,
a
variação
da
velocidade
sofrida
pelo
corpo,
que
executa
um
movimento
retilíneo
uniformemente
variado.
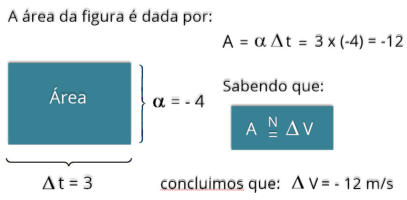
Utilizando
o
gráfico
como exemplo, vamos determinar a variação da velocidade entre os instantes
t = 1 s até t = 4 s.

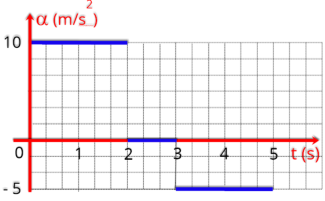
2.8.m Exercícios propostos
P8.
Dado
o
gráfico
a
seguir,
da
aceleração
em
função
do
tempo,
de
uma
partícula
que
parte
do repouso e executa um MRUV. Determine a velocidade do móvel no instante t = 5 s.
P9.
Um
móvel
executou
um
movimento
retilíneo
em
que
sua
aceleração
variou
no
tempo
conforme
o
gráfico.
A
partir
desse
gráfico,
e
considerando
que
em
t
=
0
s
a
velocidade
do
móvel era v = 0 m/s, determine no instante t = 3 s o valor da velocidade.
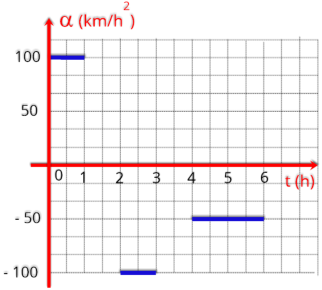
P10.
O
gráfico
da
aceleração
escalar
de
um
móvel,
em
função
do
tempo
e
realiza
um
MRUV,
é
dado na figura ao lado. Sabe-se que a velocidade inicial é nula. Determine:
a) a velocidade no instante t = 30 s,
b) a aceleração escalar média no intervalo de 0 a 40 s;
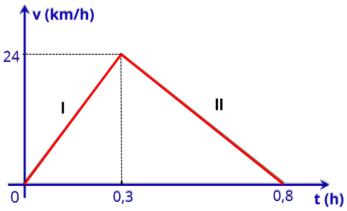
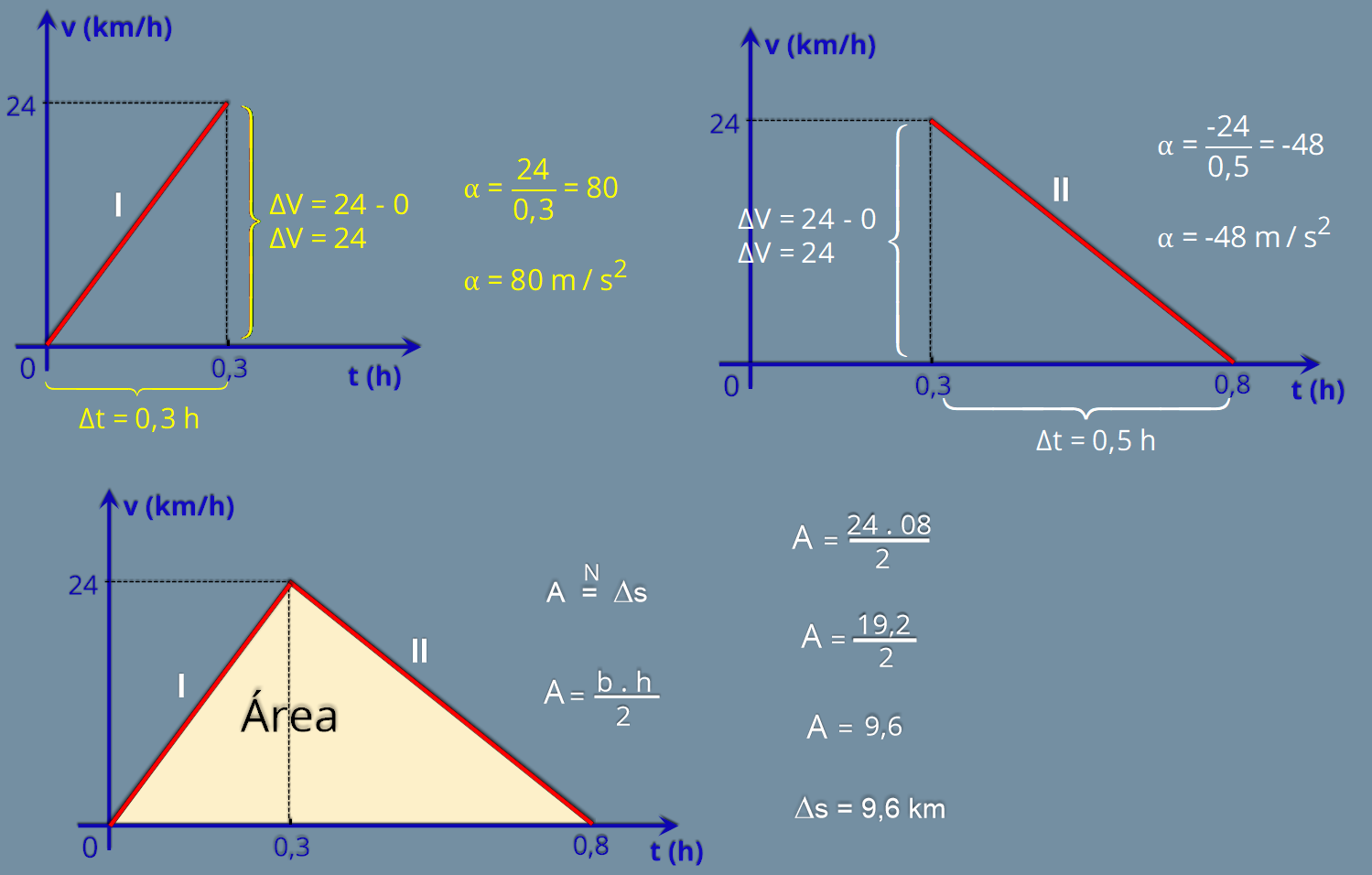
P11.
(Unicamp
-1988)
O
gráfico
v
x
t
de
um
atleta
inexperiente
numa
corrida
de
São
Silvestre
é
mostrado na figura.
a) Calcule a aceleração do atleta nos trechos I e II.
b) Calcule o espaço percorrido pelo atleta desde que começou a correr até parar.
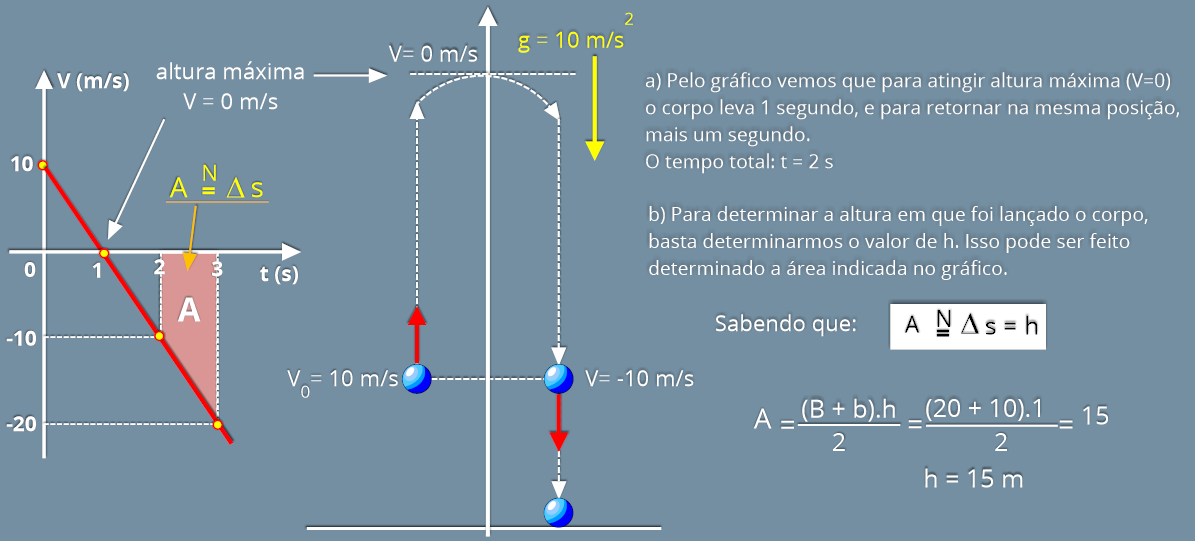
P12.
(UFRJ
2004)
De
um
ponto
localizado
a
uma
altura
h
do
solo,
lança-se
uma
pedra
verticalmente
para
cima.
A
figura
a
seguir
representa,
em
gráfico
cartesiano,
como
a
velocidade
escalar
da
pedra
varia,
em
função
do
tempo,
entre
o
instante
do
lançamento
(t
=
0)
e o instante em que chega ao solo (t = 3s).
a) Em que instante a pedra retoma ao ponto de partida? Justifique sua resposta.
b) Calcule de que altura h a pedra foi lançada.
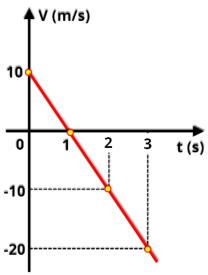
P13.
(UFPE
-
2004)
O
gráfico
da
velocidade
em
função
do
tempo
de
um
ciclista,
que
se
move
ao
longo
de
uma
pista
retilínea,
é
mostrado
a
seguir.
Considerando
que
ele
mantém
a
mesma
aceleração
entre
os
instantes
t
=
0
s
e
t
=
7
segundos,
determine
a
distância
percorrida
neste
intervalo de tempo. Expresse sua resposta em metros.
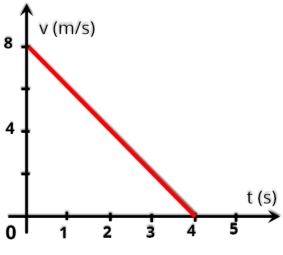
P14.
(UNESP
-
2002)
O
gráfico
na
figura
mostra
a
velocidade
de
um
automóvel
em
função
do
tempo, ao se aproximar de um semáforo que passou para o vermelho.
Determine, a partir desse gráfico,
a) a aceleração do automóvel e
b) o espaço percorrido pelo automóvel desde t = 0s até t = 4,0s.
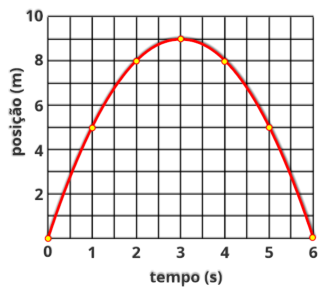
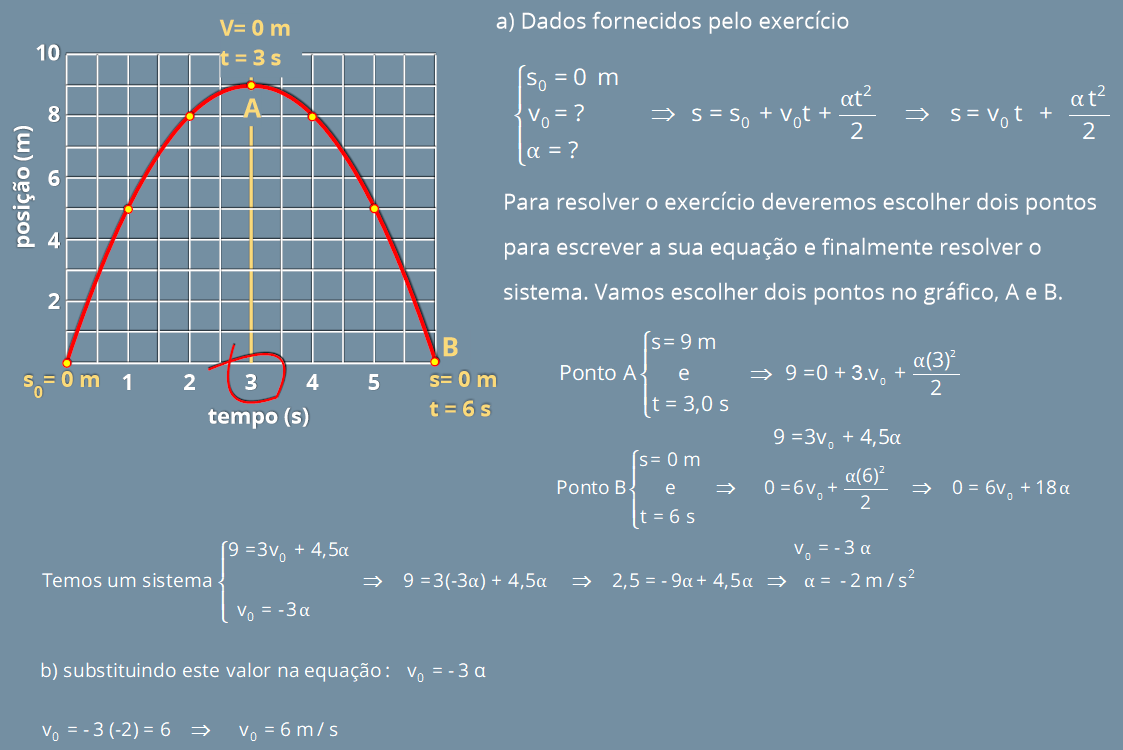
P15.
(FUVEST
-
1978)
A
figura
representa
o
gráfico
posição-tempo
do
movimento
de
um
corpo
lançado verticalmente para cima, com velocidade inicial V
0
, na superfície de um planeta.
a) Qual o valor da aceleração da gravidade na superfície do planeta?
b) Qual o valor da velocidade inicial V
0
?
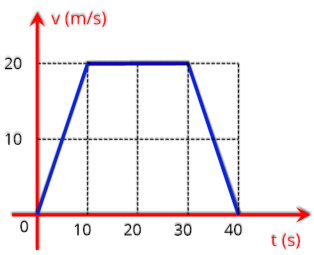
P16.
(UNESP
2003)
Um
veículo
se
desloca
em
trajetória
retilínea
e
sua
velocidade
em
função
do tempo é apresentada na figura.
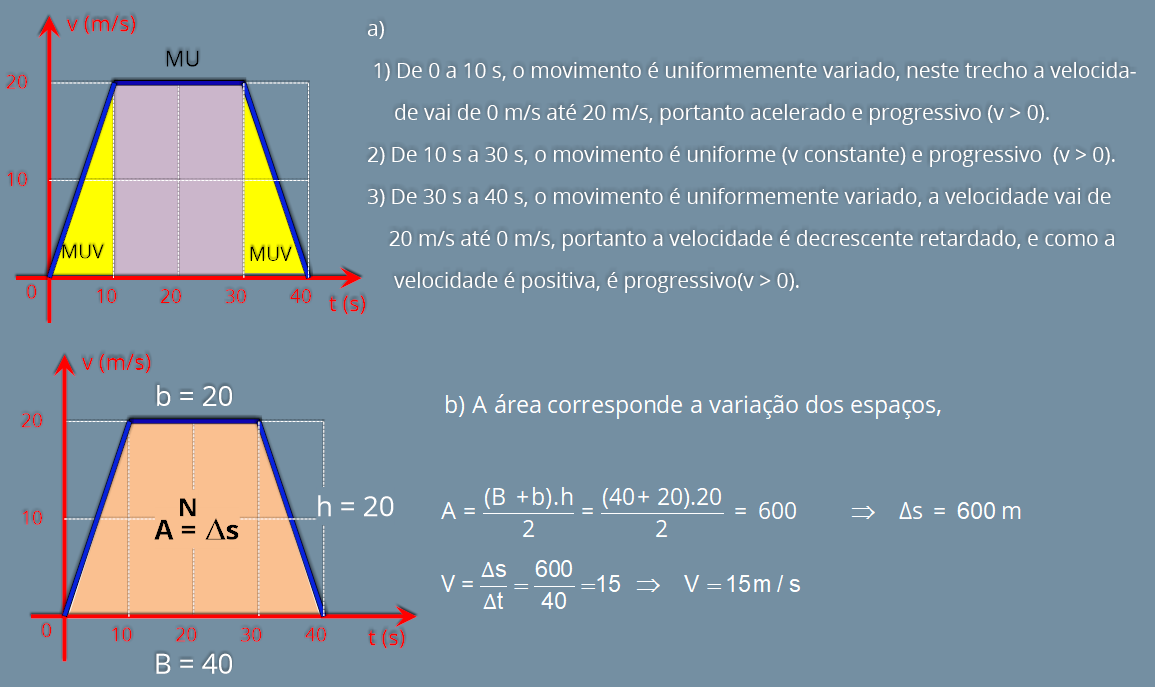
a)
Identifique
o
tipo
de
movimento
do
veículo
nos
intervalos
de
tempo
de
0
a
10
s,
de
10
a
30
s e de 30 a 40 s, respectivamente.
b) Calcule a velocidade média do veículo no intervalo de tempo entre 0 e 40 s.
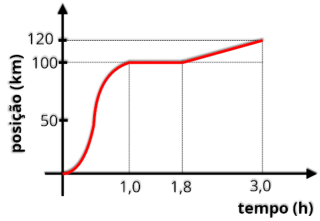
P17.
(Ufrj
2005)
A
posição
de
um
automóvel
em
viagem
entre
duas
cidades
foi
registrada
em
função
do
tempo.
O
gráfico
a
seguir
resume
as
observações
realizadas
do
início
ao
fim
da
viagem.
a) Indique durante quanto tempo o carro permaneceu parado.
b) Calcule a velocidade escalar média do carro nessa viagem.
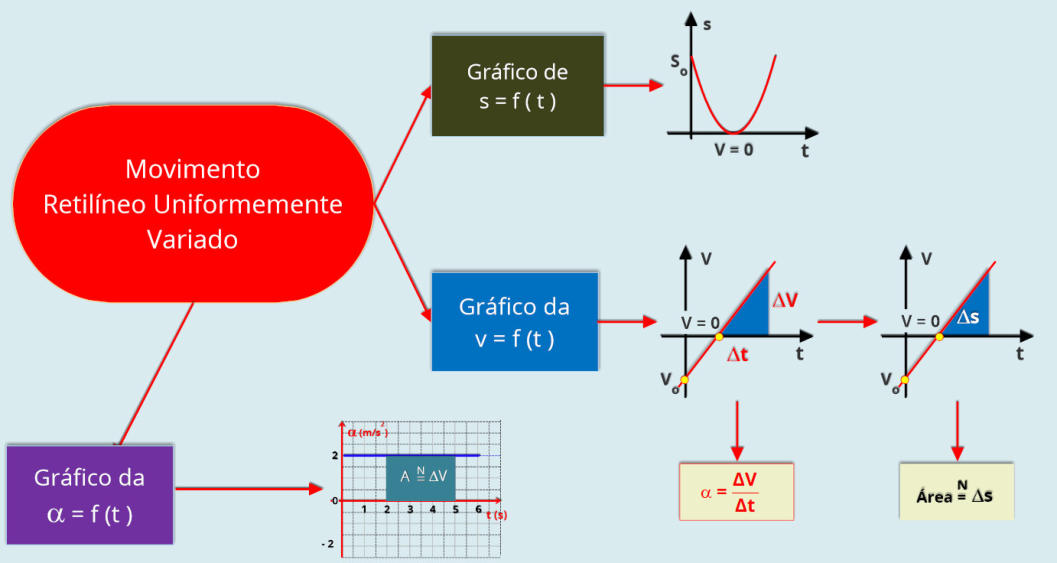
2.8.k Mapa conceitual
Este
mapa
conceitual
apresenta
uma
visão
geral
dos
exemplos
e
conceitos
vistos
nesta
página,
ele
se
apresenta
na
forma
de
um
conjunto
de
proposições
interconectadas.
O
significado
de
qualquer
conceito
é
a
soma
de
todas
as
ligações
que
contêm
o
conceito.
Para
"ler"
o
mapa
conceitual, comece do Movimento Uniformemnte Variado, e vá até os itens mais específicos e os exemplos nas partes mais externas.
Procure fazer o teu mapa conceitual, vai te ajudar a organizar os conceitos desta lição.
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
ciencia-cultura.com
Entre
os
instantes
t
=
1
s
até
t
=
3
s,
o
corpo
sofreu
um
deslocamento
de
posição
D
s = 40 m
2.8.i Determinação da variação de posição do movimento
A
construção
do
gráfico
é
feita
no
plano
cartesiano,
onde
indicamos
a
relação
entre
o
tempo
(t)
e
a
posição
(s),
através
de
dois
eixos,
como
mostra a figura acima. Poderíamos resumidamente descrever como chegamos à figura do gráfico;
Foi fornecida uma equação: s = 6 - 8t + 2.t
2
Montamos uma tabela onde demos valores para o tempo (t) e obtivemos sua respectiva posição (s).
No
plano
cartesiano,
no
eixo
horizontal
-x
na
matemática-
colocamos
os
valores
do
tempo
(t),
e
no
eixo
vertical
-eixo
y
na
matemática-
os
valores das posições (s).
Por ser uma equação do 2º grau, obtivemos uma parábola.
Nos
exercícios,
normalmente
não
nos
pedem
para
construir
um
gráfico,
o
comum
é
fornecer
um
gráfico
no
qual
deveremos
tirar
nformações sobre o movimento que ele representa.
Os
gráficos
na
cinemática
são
ferramentas
importantes
que
nos
permitem
visualizar
e
analisar
o
movimento
de
um
objeto
de
forma
clara
e
precisa.
Ao
representar
as
grandezas
físicas
envolvidas
em
um
movimento
como
posição
(
S
),
velocidade
(
V
)
e
aceleração
(
a
)
em
um
sistema
de
coordenadas,
podemos
extrair informações importantes sobre o comportamento do objeto ao longo do tempo.
Principais funções dos gráficos na cinemática:
Visualização
do
movimento:
Um
gráfico
transforma
as
equações
matemáticas
que
descrevem
o
movimento
em
imagens,
facilitando
a
compreensão
de
como
a
posição,
a
velocidade
e
a
aceleração variam com o tempo.
Identificação
do
tipo
de
movimento:
Através
da
análise
da
forma
do
gráfico,
podemos
identificar
se o movimento é uniforme, uniformemente variado ou outro tipo mais complexo.
Cálculo
de
grandezas
físicas:
A
partir
do
gráfico,
podemos
calcular
grandezas
como
velocidade
instantânea, aceleração, deslocamento total e distância percorrida.
Previsão
do
movimento:
Em
alguns
casos,
é
possível
utilizar
os
gráficos
para
prever
como
o
movimento irá se comportar em instantes futuros.
Tipos de gráficos comuns na cinemática:
Gráfico posição x tempo:
Mostra como a posição de um objeto varia ao longo do tempo.
Gráfico
velocidade
x
tempo:
Mostra
como
a
velocidade
de
um
objeto
varia
ao
longo
do
tempo.
A
área
sob
o
gráfico
representa
o
deslocamento do objeto.
Gráfico
aceleração
x
tempo:
Mostra
como
a
aceleração
de
um
objeto
varia
ao
longo
do
tempo.
A
área
sob
o
gráfico
representa
a
variação da velocidade do corpo em movimento.

ciencia-cultura.com
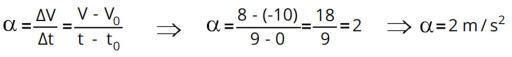
Movimentos na vertical



Na
figura
acima
indicamos
os
pontos
importantes
no
gráfico
da
posição
(s)
em
função
do
tempo
(t).
Forma
da
curva:
Uma
parábola – equação do 2º grau.
A posição inicial (S
0
) do movimento ocorre em S
0
= 21 m.
Mudança
de
sentido,
ocorre
no
instante
em
que
a
velocidade
se
anula
V
=
0
m/s,
este
instante
é
t
=
5
s
e
se
encontra
na
posição S = - 4 m.
Nesta
segunda
figura,
que
é
a
mesma
parábola,
podemos
realizar
outra
leitura
no
gráfico.
O
corpo
sai
da
posição
S
0
=
21
m,
e
vai
no
sentido
oposto
a
trajetória
até
chegar
na
posição
S
=
-4
m.
Neste
trajeto
a
velocidade
é
negativa
(V< 0).
Partindo
da
posição
S
=
-
4
m,
ele
passa
a
se
movimentar
no
sentido
da
trajetória, assim teremos a velocidade positiva (V > 0).
ciencia-cultura.com
V = - 10 + 2t








Como colaborar.
Este
site
não
possui
finan-
ciamento algum.
A
forma
que
eu
encontrei
para
arrecadar
fundos,
é
ofertar
a
compra
do
livro
indicado na figura abaixo.
Testes
da
Fuvest
com
reso-
lução comentada.













